Một hình lập phương cạnh bằng a nội tiếp khối cầu ( S 1 ) và ngoại tiếp khối cầu ( S 2 ) , gọi V 1 và V 2 lần lượt là thể tích của các khối S 1 và ( S 2 ) . Tính tỉ số k = V 1 V 2
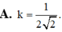
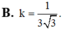
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án D
Gọi khối lập phương cần xét ABCD.A'B'C'D' cạnh a.
Bán kính mặt cầu ngoại tiếp khối cầu là R 2 = A A ' 2 = a 2 ⇒ V 1 = 4 3 R 2 3 .
Bán kính mặt cầu ngoại tiếp khối cầu là
R 1 = A C ' 2 = A B 2 + A D 2 + A A ' 2 2 = a 3 2 ⇒ V 1 = 4 3 πR 3 1
Vậy tỉ số k = V 1 V 2 = R 3 1 R 3 1 = R 1 R 2 3 = 3 3 = 3 3 .

Để ý rằng đường chéo của hình lập phương chính là đường kính của khối cầu. Mặt khác ta lại có công thức: “Bình phương độ dài đường chéo của hình lập phương bằng ba lần bình phương của độ dài cạnh hình lập phương”. Khi đó 2 R 2 = 3 a 2 ⇒ a = 2 R 3 3
Suy ra V 1 = 2 3 3 R 3 = 8 3 9 R 3 .
Vì khối cầu có bán kính R nên ta có thể tính được bán kính và chiều cao của khối trụ ngoại tiếp ngoài khối cầu lần lượt là R và 2R.
Do đó V 2 = πR 2 . 2 = 2 πR 3
Vậy ta có tỉ số V 1 V 2 = 8 3 9 R 3 2 πR 3 = 4 3 9 π ≈ 0 , 245
Đáp án C

Chọn B
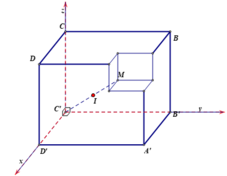
Gọi M là đỉnh của hình lập phương có cạnh bằng 1 nằm trên đường chéo AC' và nằm trên khối còn lại sau khi cắt. Gọi I là tâm của khối cầu có thể tích lớn nhất thỏa yêu cầu bài toán.
![]()
Suy ra I thuộc đoạn thẳng C'M và mặt cầu tâm I cần tìm đi qua điểm M
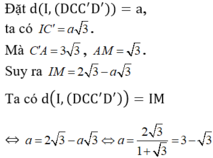
Cách khác: Chọn hệ trục tọa độ Oxyz sao cho C'(0;0;0), B' (0;3;0), D'(3;0;0), C (0;0;3).
Khi đó M(2;2;2)
Ta có phương trình đường thẳng C'M là 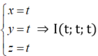 với 2 > 0 > t do I thuộc đoạn thẳng C'M
với 2 > 0 > t do I thuộc đoạn thẳng C'M
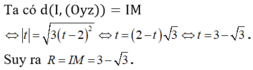

Đáp án B
Gọi M là đỉnh của hình lập phương có cạnh bằng 1 nằm trên đường chéo AC’ và nằm trên khối còn lại sau khi cắt. Gọi I là tâm của khối cầu có thể tích lớn nhất thỏa mãn yêu cầu bài toán.
Ta có d I ; A ' B ' C ' D ' = d I ; B C C ' B ' = d I ; D C C ' D '
Suy ra I thuộc đoạn thẳng C’M và mặt cầu tâm I cần tìm đi qua điểm M.
Đặt d I ; D C C ' D ' = a , ta có IC' = a 3 mà A C ' = 3 3 , A M = 3
Suy ra I M = 2 3 - a 3 mặt khác d I ; D C C ' D ' = I M ⇔ a = 2 3 - a 3 ⇒ a = 3 - 3 3

Đáp án là B.
+ Ta có: R C = a 3 ⇒ V C = 4 3 π .3 3 a 3 = 4 π a 3 3 .
+ R T = a 2 ⇒ V T = 2 a .. π 2 a 2 = 4 π a 3
Vậy V C V T = 3 .