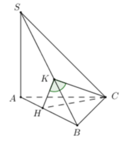
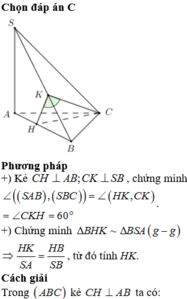
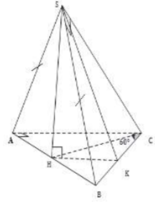
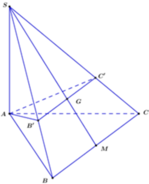
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại đỉnh A và AB = AC, SA = SB = SC = 3a. Góc giữa mặt phẳng (SAB) và mặt phẳng (ABC) là 60o. Gọi G là trọng tâm của tam giác SAB. Thể tích khối chóp S.GBC là:
A. 6 a 3 3 25
B. 6 a 3 15 25
C. a 3 3 4
D. 4 a 3 3 5 5


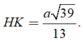
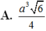
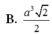
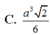
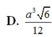

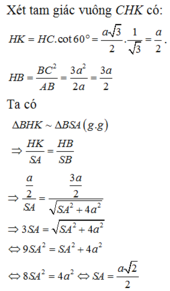
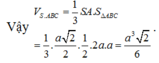

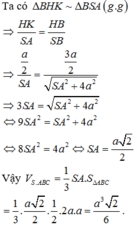
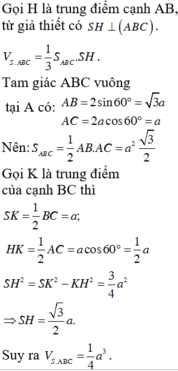

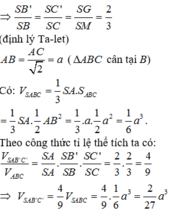
Đáp án B
Gọi H là chân đường vuông góc hạ từ đỉnh S lên mặt phẳng (ABC), khi đó ta chứng minh được H là trung điểm của BC. Gọi M là trung điểm của AB khi đó từ giả thiết ta có: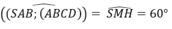
Đặt AB = x ta tính được: