Làm tính trừ các phân thức sau:
a) 2 x − 1 5 x 2 y − 4 x − 1 5 x 2 y với x ≠ 0 và y ≠ 0 ;
b) y + 8 y 2 − 16 − 2 y 2 + 4 y với y ≠ 0 và y ≠ ± 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

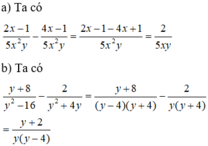

\(a,\dfrac{x}{x+3}+\dfrac{2-x}{x+3}\\ =\dfrac{x+2-x}{x+3}\\ =\dfrac{2}{x+3}\\b,\dfrac{x^2y}{x-y}-\dfrac{xy^2}{x-y}\\ =\dfrac{x^2y-xy^2}{x-y}\\ =\dfrac{xy\left(x-y\right)}{x-y}\\ =xy\\ c,\dfrac{2x}{2x-y}+\dfrac{y}{y-2x}\\=\dfrac{2x}{2x-y}-\dfrac{y}{2x-y}\\ =\dfrac{2x-y}{2x-y}\\ =1 \)
`a, x/(x+3) + (2-x)/(x+3) = (x+2-x)/(x+3) = 2/(x+3)`
`b, (x^2y)/(x-y) - (xy^2)/(x-y) = (x^2y-xy^2)/(x-y) = (xy(x-y))/(x-y)= xy`
`c, (2x)/(2x-y) - (y)/(2x-y)`
`= (2x-y)/(2x-y) = 1`

a: \(=\dfrac{3b+4a}{6ab}\)
b: \(=\dfrac{x^2-2x+1-x^2-2x-1}{x^2-1}=\dfrac{-4x}{x^2-1}\)
c: \(=\dfrac{xz+yz-xy-xz}{xyz}=\dfrac{yz-xy}{xyz}=\dfrac{z-x}{xz}\)
d: \(=\dfrac{2x+6-12}{\left(x-3\right)\left(x+3\right)}=\dfrac{2x-6}{\left(x-3\right)\left(x+3\right)}=\dfrac{2}{x+3}\)
e: \(=\dfrac{x-2+2}{\left(x-2\right)^2}=\dfrac{x}{\left(x-2\right)^2}\)

a, \(x^2-2x+5\)
Với x = 1 => \(1-2+5=4\)
Với x = -2 => \(4-2\left(-2\right)+5=13\)
b, \(2x^2+4y^3-3xy+2\)
Với y = 1 ; x = 1 => \(2+4-3+2=5\)
Với x = -3 ; y = 5 => \(2.9+4.125-3.\left(-3\right).5+2=18+500+45+2=565\)

a) \(\dfrac{3x^2y}{2xy^5}=\dfrac{3x}{2y^4}\)
b) \(\dfrac{3x^2-3x}{x-1}=\dfrac{3x\left(x-1\right)}{x-1}=3x\)
c) \(\dfrac{ab^2-a^2b}{2a^2+a}=\dfrac{ab\left(b-a\right)}{a\left(2a+1\right)}=\dfrac{b\left(b-a\right)}{2a+1}=\dfrac{b^2-ab}{2a+1}\)
d) \(\dfrac{12\left(x^4-1\right)}{18\left(x^2-1\right)}=\dfrac{2\left(x^2-1\right)\left(x^2+1\right)}{3\left(x^2-1\right)}=\dfrac{2\left(x^2+1\right)}{3}\)
`a, (3x^2y)/(2xy^5)`
`= (3x)/(2y^4)`
`b, (3x^2-3x)/(x-1)`
`= (3x(x-1))/(x-1)`
`= 3x`
`c, (ab^2-a^2b)/(2a^2+a)`
`= (b(a-b))/((2a+1))`
`d, (12(x^4-1))/(18(x^2-1)) = (2(x^2+1))/3`.

a) P(x) = \(2{x^3} + 5{x^2} - 4x + 3\) thay x = -2 vào đa thức ta có :
\(P(-2)= 2{(-2)^3} + 5{(-2)^2} - 4.(-2)+ 3 = 2.( - 8) + 5.4 - 4.( - 2) + 3 = 15\)
b) Q(y) =\(2{y^3} - {y^4} + 5{y^2} - y\) thay y = 3 vào đa thức ta có :
\(Q(3)=2{3^3} - {3^4} + 5{3^2} - 3 = 2.27 - 81 + 5.9 - 3 = 15\)

\(a,\dfrac{x+2}{x-1}-\dfrac{x-3}{x-1}-\dfrac{x-4}{1-x}\\ =\dfrac{x+2}{x-1}-\dfrac{x-3}{x-1}+\dfrac{x-4}{x-1}\\ =\dfrac{x+2-x+3+x-4}{x-1}\\ =\dfrac{x+1}{x-1}\)
\(b,\dfrac{1}{x+5}-\dfrac{1}{x-5}+\dfrac{2x}{x^2-25}\\ =\dfrac{1}{x+5}-\dfrac{1}{x-5}+\dfrac{2x}{\left(x-5\right)\left(x+5\right)}\\ =\dfrac{x-5-x-5+2x}{\left(x-5\right)\left(x+5\right)}\\ =\dfrac{2x-10}{\left(x-5\right)\left(x+5\right)}\\ =\dfrac{2\left(x-5\right)}{\left(x-5\right)\left(x+5\right)}\\ =\dfrac{2}{x+5}\)
\(c,x+\dfrac{2y^2}{x+y}-y\\ =\dfrac{x\left(x+y\right)+2y^2-y\left(x+y\right)}{x+y}\\ =\dfrac{x^2+xy+2y^2-xy-y^2}{x+y}\\ =\dfrac{x^2+y^2}{x+y}\)

\(a,2\left(x-1\right)\left(x+1\right)+\left(x-1\right)^2+\left(x+1\right)^2\)
\(=2\left(x^2-1\right)+x^2-2x+1+x^2+2x+1\)
\(=2x^2-2+2x^2+2=4x^2\)
\(b,\left(x-y+1\right)^2+\left(1-y\right)^2+2\left(x-y+1\right)\left(y-1\right)\)
\(=\left(x-y+1\right)^2+2\left(x-y+1\right)\left(y-1\right)+\left(y-1\right)^2\)
\(=\left[\left(x-y+1\right)+\left(y-1\right)\right]^2\)
\(=\left[x-y+1+y-1\right]^2=x^2\)
đề cuối phải sửa cái cuối thành \(\left(3x+5\right)^2\)
\(c,\left(3x+1\right)^2-2\left(3x+1\right)\left(3x+5\right)+\left(3x+5\right)^2\)
\(=\left[\left(3x+1\right)-\left(3x+5\right)\right]^2=\left[3x+1-3x-5\right]^2=16\)

Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người đọc hiểu đề của bạn hơn nhé.
a: \(\dfrac{1}{2a}+\dfrac{2}{3b}\)(ĐKXĐ: a<>0 và b<>0)
\(=\dfrac{1\cdot3b+2\cdot2a}{2a\cdot3b}\)
\(=\dfrac{3b+4a}{6ab}\)
b: \(\dfrac{x-1}{x+1}-\dfrac{x+1}{x-1}\)(ĐKXĐ: \(x\notin\left\{1;-1\right\}\))
\(=\dfrac{\left(x-1\right)^2-\left(x+1\right)^2}{\left(x+1\right)\left(x-1\right)}\)
\(=\dfrac{x^2-2x+1-x^2-2x-1}{\left(x+1\right)\left(x-1\right)}=\dfrac{-4x}{x^2-1}\)
c: \(\dfrac{x+y}{xy-y}+\dfrac{z}{yz}\)(ĐKXĐ: \(\left\{{}\begin{matrix}x< >1\\y< >0\\z< >0\end{matrix}\right.\))
\(=\dfrac{x+y}{y\left(x-1\right)}+\dfrac{1}{y}\)
\(=\dfrac{x+y+x-1}{y\left(x-1\right)}\)
\(=\dfrac{2x+y-1}{y\left(x-1\right)}\)
d: ĐKXĐ: \(x\notin\left\{3;-3\right\}\)
\(\dfrac{2}{x-3}-\dfrac{12}{x^2-9}\)
\(=\dfrac{2}{x-3}-\dfrac{12}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{2x+6-12}{\left(x-3\right)\left(x+3\right)}=\dfrac{2x-6}{\left(x-3\right)\left(x+3\right)}=\dfrac{2}{x+3}\)
e: ĐKXĐ: x<>2
\(\dfrac{1}{x-2}+\dfrac{2}{x^2-4x+4}\)
\(=\dfrac{1}{x-2}+\dfrac{2}{\left(x-2\right)^2}\)
\(=\dfrac{x-2+2}{\left(x-2\right)^2}=\dfrac{x}{\left(x-2\right)^2}\)

\(a,=\dfrac{4y.5x^3}{3x^2.2y^3}=\dfrac{20x^3y}{6x^2y^3}=\dfrac{10x}{3y^2}\\ b,=\dfrac{\left(x-1\right)^2.x\left(x+1\right)}{\left(x-1\right)\left(x+1\right)\left(x-1\right)}=\dfrac{\left(x-1\right)^2.x.\left(x+1\right)}{\left(x-1\right)^2.\left(x+1\right)}=x\)
\(c,=\dfrac{x\left(2+x\right).3\left(x^3+1\right)}{\left(x^2-x+1\right).3.\left(x+2\right)}=\dfrac{3x.\left(x+2\right).\left(x+1\right)\left(x^2-x+1\right)}{\left(x^2-x+1\right).3\left(x+2\right)}=x\left(x+1\right)\)