Cho hình bình hành ABCD có diện tích là S. Gọi M là trung điểm của BC. Gọi N là giao điểm của AM và BD. Tính diện tích tứ giác MNDC theo S
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


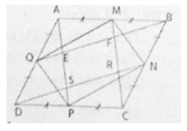
a) Ta có AB // CD (gt)
Suy ra AM // CP (1)
Lại có AM = AB/2; CP = CD/2 (2)
Từ (1) và (2) suy ra AMCP là hình bình hành
Suy ra AP // CM hay ES // FR.
Tương tự ta cũng chứng minh được tứ giác BQDN là hình bình hành nên BQ // DN. Suy ra EF // RS.
Vậy tứ giác EFRS là hình bình hành
b) Đặt PS = x. Suy ra CR = 2x (tính chất đường trung bình)
Từ đó suy ra RF = ES = AE = 2x
Suy ra: ES = 2AP/5 => SEFRS = 2SAMCP/5
Vì SAMCP = SABCD/2 nên SEFRS = SABCD/2

tự vẽ hình nhé bạn
a) xét tg ABMN có
AN = BM ( bạn tự c/m)
AN // BM ( bạn tự c/m)
==> ABMN hbh
mà AN = AB ==> ABMN hthoi ==> góc P = 90 độ
==> KB // DM ( cug vuông vs PM)
==> MDKB hthang
b) c/m t2 ta có NMDC hthoi ==> góc Q = 90 độ
Xét tam giác ADM có AN = ND = NM ( ABMN hthoi)
==> ADM tam giác vuông ( Đ.lý Py ta go đảo)
==> góc M = 90 độ
ta có góc P = góc M = góc Q = 90 độ ==> PMQN hcn
c) Shcn PMQN = PM . MQ = 8 . 5 = 40 cm2
d) ( tự c/m :P)
dc thì like nhé :)))
Gọi I là trung điểm của AD, K là giao điểm của CI và BD. Kẻ ME ^ BD tại E, CF ^ BD tại F.
Có B N = 1 3 B D , E M = 1 2 C F S B M N = 1 2 E M . B N = 1 2 . 1 2 C F . 1 3 B D = 1 6 S B C D = 1 12 S ⇒ S M N D C = 1 2 S − 1 12 S = 5 12 S