Tính số êlectron bị bật ra khỏi catôt của một tế bào quang điện trong mỗi giây khi cường độ của dòng quang điện bão hòa là 40mA. Chọn đáp án đúng:
A. 3,5.1014 hạt e
B. 2,5.1014 hạt e
C. 4,5.1014 hạt e
D. 1,5.1014 hạt e
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Giới hạn quang điện: \(\lambda_0=\dfrac{hc}{A_t}=\dfrac{6,625.10^{-34}.3.10^8}{2,48.1,6.10^{-19}}=0,5.10^{-6}=0,5\mu m\)
b. Áp dụng công thức Anhxtanh về hiện tượng quang điện: \(\dfrac{hc}{\lambda}=A_t+\dfrac{1}{2}mv^2\)
\(\dfrac{6,625.10^{-34}.3.10^8}{0,36.10^{-6}}=2,48.1,6.10^{-19}+\dfrac{1}{2}9,1.10^{-31}v^2\) \(\Rightarrow v\)
c. Cường độ dòng điện bão hòa: \(I_{bh}=n.1,6.10^{-19}=0,3.10^{-6}\Rightarrow n = 1,875.10^{12}\)(hạt/s)
d. Điện áp hãm: \(eU_h=W_{đmax}\Rightarrow U_h\)

- Vì cứ 100 photon tới catôt thì có 1 êlectron bứt ra khỏi catôt nên trong mỗi giây, số êlectron bứt ra khỏi catôt là:
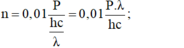
- Khi đó cường độ dòng quang điện bão hòa có giá trị là:
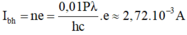

a. Bước sóng của chùm sáng: \(\lambda=\dfrac{c}{f}=\dfrac{3.10^8}{10^{15}}=0,3\mu m\)
Giới hạn quang điện: \(\lambda_0=\dfrac{hc}{A_t}=\dfrac{6,625.10^{-34}.3.10^8}{5,15.1,6.10^{-19}}=0,24.19^-6m=0,24\mu m\)
Do \(\lambda > \lambda_0\) nên không xảy ra hiện tượng quang điện.
b. Ta có: \({W_{d0}} = \frac{{hc}}{\lambda } - A = 1,{7.10^{ - 19}}J\Rightarrow {v_0} = \sqrt {\frac{{2{W_{d0}}}}{m}} = 0,{6.10^6}m/s\)
c. \({n_e} = \frac{{{I_{bh}}}}{e} = 2,{8.10^{13}};\,\,\,\,\,\,{n_\lambda } = \frac{P}{{\frac{{hc}}{\lambda }}} = \frac{{P\lambda }}{{hc}} ={3.10^{15}} \Rightarrow H = \frac{{{n_e}}}{{{n_\lambda }}} = 9,{3.10^{ - 3}} = 0,93\% \)

Đáp án: A
Ta có
N e = I b h e = 64 . 10 - 6 1 , 6 . 10 - 19 = 4 . 10 14 ( ê l e c t r o n ) H = N e N p . 100 % = 0 , 2 % ⇒ N p = 100 % N e 2 % = 50 N e = 50 . 4 . 10 14 = 2 . 10 16 ( p h ô t ô n / g i â y )
Đáp án: B
Điện lượng chuyển qua tế bào quang điện trong một giây:
Số êlectron bật ra khỏi catôt trong 1 giây: