Một viên đạn khối lượng m = 10g bay theo phương ngang với vận tốc v = 40m/s đến va chạm đàn hồi xuyên tâm vào một quả cầu khối lượng M = 190g được treo bằng một sợi dây nhẹ, mềm và không dãn dài l. Kết quả là làm cho sợi dây bị lệch đi một góc lớn nhất
α
0
= 60° so với phương thẳng đứng. Giá trị của bằng A. 0,4 m B. 0,8 m C. 0,2 m D. 1,2...
Đọc tiếp
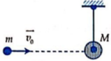
Một viên đạn khối lượng m = 10g bay theo phương ngang với vận tốc v = 40m/s đến va chạm đàn hồi xuyên tâm vào một quả cầu khối lượng M = 190g được treo bằng một sợi dây nhẹ, mềm và không dãn dài l. Kết quả là làm cho sợi dây bị lệch đi một góc lớn nhất α 0 = 60° so với phương thẳng đứng. Giá trị của bằng
A. 0,4 m
B. 0,8 m
C. 0,2 m
D. 1,2 m
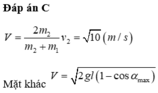
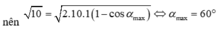
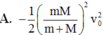
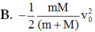
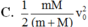
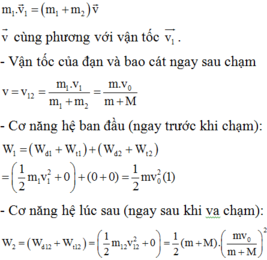
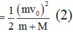
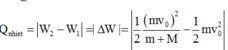
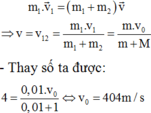
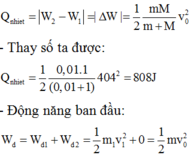
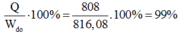
Đáp án A
- Chọn mốc thế năng hấp dẫn là vị trí va chạm
- Xét thời điểm ngay khi va chạm đàn hồi giữa m và M là hệ kín
- Áp dụmg định luật bảo toàn động lượng và cơ năng cho hệ ta có
- Thay số ta được vận tốc của M ngay sau va chạm là:
Bảo toàn cơ năng cho con lắc M gắn dây, sau khi va chạm vật M chuyển động lên đến vị trí dây treo lệch
với phương thẳng đứng một góc lớn nhất ứng với thế năng lớn nhất động năng bằng không vậy ta có: