Cho hình lăng trụ ABC.A'B'C' Gọi E, F lần lượt là trung điểm của BB¢ và CC¢. Mặt phẳng (AEF) chia khối lăng trụ thành hai phần có thể tích V 1 và V 2 như hình vẽ.
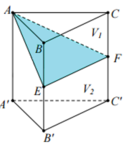
Tỉ số V 1 V 2 là
A. 1 2
B. 1
C. 1 3
D. 1 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Dễ thấy VA.BCC’B’ = 1 2 VABC.A’B’C’
Lại có VA.BCFE = 1 2 VA.BCC’B’
=> VA.BCFE = . VABC.A’B’C’

Đáp án A
V 1 = 1 3 d A ; B C C ' B ' . S B E F C = 1 3 d A ; B C C ' B ' . S B C C ' B ' = 1 2 V A B C C ' B '
Mà:
V A B C . A ' B ' C ' = V A . A ' B ' C ' + V A . B C C ' B ' ⇒ V A B C ' C ' B ' = 2 3 V A B C . A ' B ' C ' ⇒ V 1 = 1 2 . 2 3 V A B C . A ' B ' C ' = 1 3 V A B C . A ' B ' C '
Mặt khác:
V 1 + V 2 = V A B C . A ' B ' C ' → V 2 = 2 3 V A B C . A ' B ' C ' ⇒ V 1 V 2 = 1 3 : 2 3 = 1 2

Đáp án B
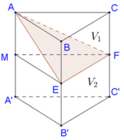
Gọi M là trung điểm của AA’. Gọi V là thể tích của hình lăng trụ ABC.A’B’C’
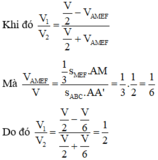

Chọn B
Gọi M là trung điểm của AA’. Gọi V là thể tích của hình lăng trụ ABC.A’B’C’
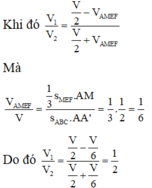

Chọn B
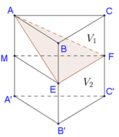
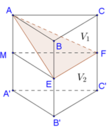
Gọi M là trung điểm của AA’. Gọi V là thể tích của hình lăng trụ ABC.A’B’C’
Khi đó
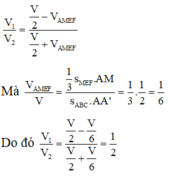

Đáp án D.
Ta có: S B M C N = B M + C N 2 d B B ' ; C C ' = B B ' 2 + 3 4 C C ' 2 d B B ' ; C C ' = 5 8 B B ' . d B B ' ; C C '
Do đó V 2 = 5 8 V A . B C C ' B ' = 5 8 . 2 3 V (với V = V A B C . A ' B ' C ' ) = 5 12 V
Suy ra V 1 = 7 12 V ⇒ V 1 V 2 = 7 5 .