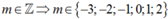Hỏi có bao nhiêu giá trị nguyên của m để phương trình m( 2x + 3x) = 3x+1- 2x+2 có nghiệm thực?
A.8
B.5
C.7
D. 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn D.
Phương pháp: Biện luận nghiệm của phương trình theo m.
Cách giải: Ta có:



Chọn A.
Phương trình đã cho tương đương 3x= -m2+10m-9 (1)
Phương trình (1) có nghiệm thực khi và chỉ khi -m2+10m -9>0 hay 1<m<9
Mà ![]()

Chọn đáp án B
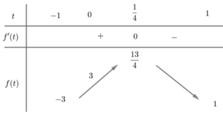
Phương trình tương đương với:
![]() (1)
(1)
Đặt t = x 2 - 2 x + m , phương trình (1) đưa được về hệ:
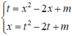
Trừ theo vế của hai phương trình trong hệ trên, ta được:
![]()
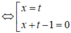
Suy ra
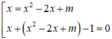
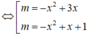
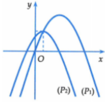
Vẽ trên cùng một hệ trục tọa độ Oxy hai đường parabol P 1 : y = - x 2 + 3 x và P 2 : y = - x 2 + x + 1 (hình vẽ bên).
Xét phương trình hoành độ giao điểm của (P1) và (P2):
![]()
![]()
Suy ra (P1) cắt (P2) tại điểm 1 2 ; 5 4 .
Để phương trình đã cho có bốn nghiệm phân biệt
Đường thẳng y = m cắt (P1) tại hai điểm và cắt (P2) tại hai điểm.
Quan sát đồ thị ta thấy m ≤ 5 4 .
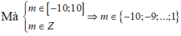
Vậy có 12 giá trị của m thỏa mãn yêu cầu bài toán.
Chọn D.
Phương trình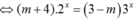
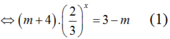
YCBT trở thành(1) có nghiệm thực khi và chỉ khi (m + 4) (3 - m) > 0
Suy ra: -4 < m < 3
Mà