Cho hình chóp S.ABCD có đáy ABCD là hình thoi, O là giao điểm của 2 đường chéo và SA = SC. Các khẳng định sau, khẳng định nào đúng?
A. S A ⊥ A B C D
B. B D ⊥ S A C
C. A C ⊥ S B D
D. A B ⊥ S A C
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Vì S A ⊥ ( A B C D ) nên AC là hình chiếu vuông góc của SC lên(ABCD).
Góc giữa giữa SC và mp (ABCD) bằng góc SC&AC ⇒ α = SCA.
Xét tam giác SAC vuông tại A có
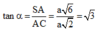
⇒ α = 60 o

Vì S A ⊥ A B C D nên AC là hình chiếu vuông góc của SC lên (ABCD).
Góc giữa giữa SC và mp (ABCD) bằng góc SC&AC ⇒ α = SCA.
Xét tam giác SAC vuông tại A có
tan α = S A A C = a 6 a 2 = 3 ⇒ α = 60 o
Chọn D

Đáp án B
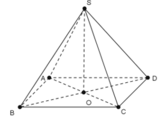
+) Tam giác SAC cân tại S có SO là trung tuyến
⇒ SO cũng là đường cao ⇒ SO ⊥ AC.
+) Tam giác SBD cân tại S có SO là trung tuyến
⇒ SO cũng là đường cao ⇒ SO ⊥ BD.
- Từ đó suy ra SO ⊥ (ABCD).
→ Do ABCD là hình thoi nên CD không vuông góc với BD. Do đó CD không vuông góc với (SBD).
Chọn C.
- Ta có: SA = SC nên SAC là tam giác cân tại S.
- Mặt khác: đáy ABCD là hình thoi có O là giao điểm hai đường chéo nên O là trung điểm của AC .
- Khi đó ta có: AC ⊥ SO.