Vẽ các đường thẳng (d1) y=x-2 và (d2) \(y = -{3 \over 2}x+3\) trên cùng một mặt phẳng tọa độ và chứng minh chúng cắt nhau tại điểm A trên trục hoành.b) Gọi giao điểm của (d1) và (d2) với trục tung là B và C. Tính các góc của tam giác ABC.c) Tính chu vi và diện tích của tam giác...
Đọc tiếp
Vẽ các đường thẳng (d1) y=x-2 và (d2) \(y = -{3 \over 2}x+3\) trên cùng một mặt phẳng tọa độ và chứng minh chúng cắt nhau tại điểm A trên trục hoành.
b) Gọi giao điểm của (d1) và (d2) với trục tung là B và C. Tính các góc của tam giác ABC.
c) Tính chu vi và diện tích của tam giác ABC.
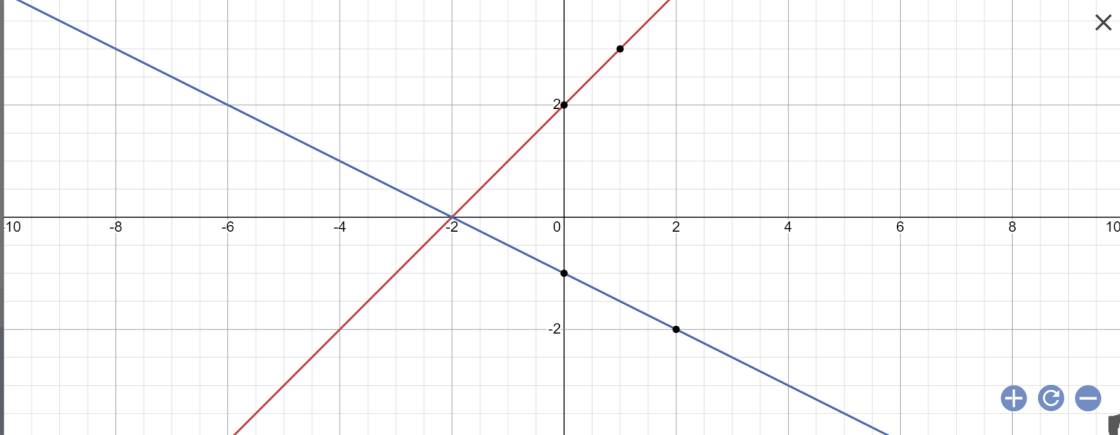
b, Gọi giao điểm của 2 đường thẳng trên là M(x1;y1)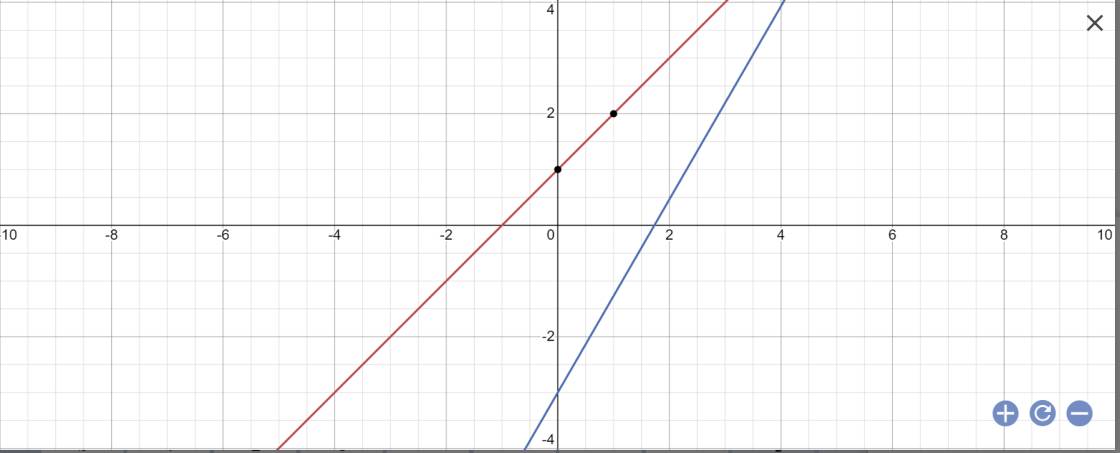
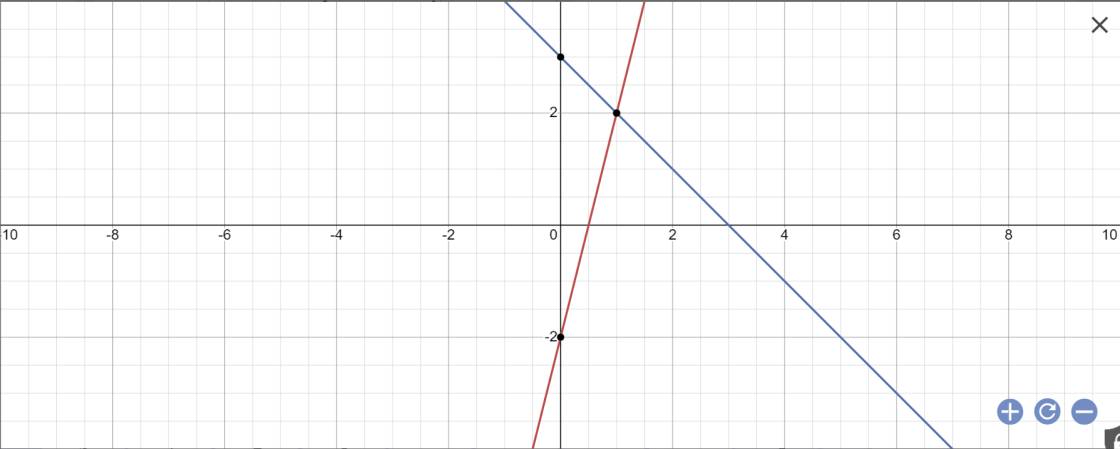
a) (d1): y = (m+2)x - m + 1 có hệ số a1 = m+2, b1 = -m +1
(d2): y = (2m-5)x + m có hệ số a2 = 2m - 5, b2 = m
Vậy khi m = 7 thì (d1) song song với (d2)
Bài 2: Cho đường thẳng (AB): y = -1/3x + 2/3; (BC): y = 5x+1; (CA): y = 3x. Xác định tọa độ ba đỉnh của tam giác ABC
Hướng dẫn giải
Điểm B là giao điểm của (AB) và (BC):
Phương trình hoành độ giao điểm B:
Điểm A là giao điểm của (AB) và (AC) nên:
Phương trình hoành độ giao điểm A:
-1/3x + 2/3 = 3x
⇔ 3x + 1/3x = 2/3
⇔ x.10/3 = 2/3
⇔ x = 1/5
=> y = 3.1/5 = 3/5
Vậy A(1/5;3/5)
Điểm C là giao điểm của (BC) và (AC) nên:
Phương trình hoành độ giao điểm C:
5x + 1 = 3x
⇔ 2x = -1
⇔ x = -1/2
> y = 3.(-1/2) = -3/2
Vậy C(-1/2;-3/2)