Cho hai con lắc lò xo mắc vào hai mặt tường đối diện nhau và cùng đặt trên mặt phẳng nhẵn nằm ngang, các lò xo có độ cứng lần lượt là
100
N
/
m
và
400
N
/
m
. Vật nặng ở hai con lắc có khối lượng bằng nhau. Kéo vật thứ nhất về bên trái, vật thứ hai về bên phải rồi buông nhẹ để hai vật dao động cùng năng lượng
0
,
25
J
. Biết khoảng cách...
Đọc tiếp
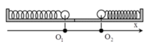
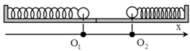
Cho hai con lắc lò xo mắc vào hai mặt tường đối diện nhau và cùng đặt trên mặt phẳng nhẵn nằm ngang, các lò xo có độ cứng lần lượt là 100 N / m và 400 N / m . Vật nặng ở hai con lắc có khối lượng bằng nhau. Kéo vật thứ nhất về bên trái, vật thứ hai về bên phải rồi buông nhẹ để hai vật dao động cùng năng lượng 0 , 25 J . Biết khoảng cách lúc đầu của hai vật là 10cm. Xác định khoảng cách ngắn nhất giữa hai vật trong quá trình dao động:
A. 4,69cm
B. 5cm
C. 7,5cm
D. 10cm
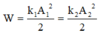
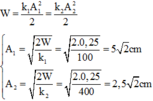
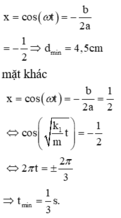
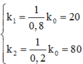
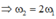
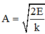
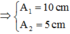
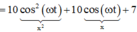
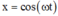
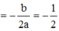
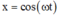
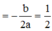
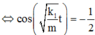
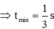
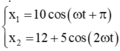
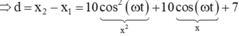
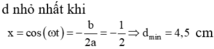
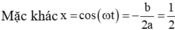
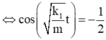
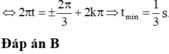
Đáp án A
Biên độ dao động của vật tính từ công thức: W = k 1 A 1 2 2 = k 2 A 2 2 2
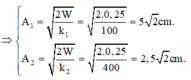
⇒ A 1 = 2 W k 1 = 2.0 , 25 100 = 5 2 c m A 2 = 2 W k 2 = 2.0 , 25 400 = 2 , 5 2 c m
Khoảng cách lúc đầu giữa hai vật là: 10cm
Chọn gốc thời gian là lúc bắt đầu dao động, chọn gốc tọa độ trùng với O 1 thì phương trình dao động của các vật lần lượt là: x 1 = − 5 2 cos ω t và x 2 = 10 + 2 , 5 2 cos 2 ω t = 10 + 2 , 5 2 2 cos 2 ω t − 1
Khoảng cách giữa hai vật: y = x 2 − x 1 = 5 2 cos 2 ω t + 5 2 cos ω t + 10 − 2 , 5 2
Ta thấy y là tam thức bậc hai đối với cos ω t và y min ⇔ cos ω t = − 0 , 5 .
Thay vào biểu thức ta tính được y = 5 2 . − 0 , 5 2 + 5 2 . − 0 , 5 + 10 − 2 , 5 2 = 4 , 69 c m