Cho hình chóp S.ABCDcó đáy ABCD là hình vuông cạnh a, S A ⊥ A B C D và S A = x . Tìm giá trị của x để góc giữa hai mặt phẳng (SBC) và (SCD) bằng 60 0 .
A. x = 2 a .
B. x = 3 a 2 .
C. x = a 2 .
D. x = a .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
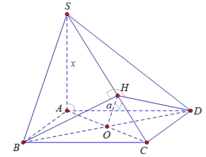
- Kẻ BH ⊥ SC ⇒ DH ⊥ SC (hai đường cao tương ứng của hai tam giác bằng nhau).
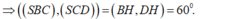
- Có 2 trường hợp xảy ra:
TH1:
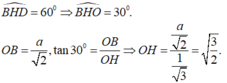
- Xét hai tam giác đồng dạng SAC và OHC ta có

TH2:
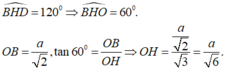
- Xét hai tam giác đồng dạng SAC và OHC ta có:
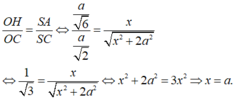

Chọn B
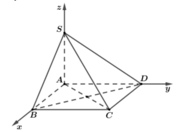
Để cho gọn ta chọn a =1
Chọn hệ trục tọa độ sao cho A = O(0;0;0) và B(1;0;0), D(0;1;0) S(0;0;x) với x = SA >0
Suy ra C(1;1;0)
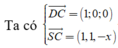
=> VTPT của mặt phẳng (SCD) là
![]()
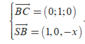
=> VTPT của mặt phẳng (SBC) là
![]()
Từ giả thiết bài toán, ta có
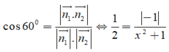
![]()

Đáp án C
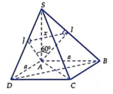
+ Trong S A B dựng A I ⊥ S B ta chứng minh được A I ⊥ S B C 1 .
Trong S A D dựng A J ⊥ S D ta chứng minh được A J ⊥ S C D 2 .
Từ (1) và (2) ⇒ S B C , S C D ^ = A I , A J ^ = I A J ^
+ Ta chứng minh được A I = A J . Do đó, nếu góc I A J ^ = 60 ° thì Δ A I J đều ⇒ A I = A J = I J .
Δ S A B vuông tại A có AI là đường cao ⇒ A I . S B = S A . A B ⇒ A I = S A . A B S B 3
Và có S A 2 = S I . S B ⇒ S I = S A 2 S B 4
Ta chứng minh được I J // B D ⇒ I J B D = S I S B ⇒ I J = S I . B D S B = 4 S A 2 . B D 2 S B 2 5 .
Thế (3)&(5) vào A I = I J ⇒ A B = S A . B D S B ⇔ A B . S B = S A . B D .
⇔ a . x 2 + a 2 = x . a 2 ⇔ x 2 + a 2 = 2 x 2 ⇔ x = a

gọi K thuộc SC sao cho DK \(\perp\) SC , BK \(\perp\)SC
=> ((SCD),(SBC)) = (DK,KB)
tính được SD = \(\frac{\sqrt{10}}{2}\)a, AC = \(\sqrt{3}\)a, SC= \(\frac{3\sqrt{2}}{2}\)a
\(DC^2=SD^2+SC^2-2SD.SC.cos\widehat{DSC}\)
=> \(\widehat{DSC}\)=....... (số xấu)
\(sin\widehat{DSC}\)= \(\frac{DK}{SD}\)=> DK = \(\frac{\sqrt{2}}{2}\)=BK
\(DB^2=DK^2+BK^2-2.DK.BK.cos\alpha\)=> \(\alpha=\frac{\pi}{2}\)

Gọi O là tâm hình vuông và H là hình chiếu của O lên SC
Ta có O H D ^ = 60 o ( D H B ^ là góc giữa hai mặt phẳng (SCD) và (SBC) )
Diện tích của ∆ S O C là
x a 2 2 = O H . S C ⇒ O H = x a 2 2 x 2 + 2 a a O H = a 2 2 . 1 3
Do đó x = a
Đáp án A
Đáp án D
Hạ H, K lần lượt là hình chiếu vuông góc của A xuống SB và SD.
Ta có:
A H ⊥ S B A H ⊥ B C ⇒ A H ⊥ S B C . Tương tự A K ⊥ S D C
Như vậy S B C , S D C ^ = A H , A K ^ = H A K ^
Ta có Δ S A B = Δ S A D suy ra A H = A K . Vì góc giữa hai mặt phẳng (SBC) và (SCD) bằng 60 0 nên ΔAHK đều.
Ta có S H S B = S K S D = H K B D , mà S H S B = S A 2 S B 2 = x 2 x 2 + a 2 = K H a 2 suy ra K H = a 2 x 2 x 2 + a 2 .
Ta lại có 1 A H 2 = 1 S A 2 + 1 A B 2 = a 2 + x 2 a 2 x 2 suy ra A H 2 = a 2 x 2 a 2 + x 2 .
ΔAHK đều nên ta có
K H 2 = A H 2 ⇔ a 2 x 2 x 2 + a 2 2 = a 2 x 2 a 2 + x 2 ⇔ x = a .
Vậy x = a thì góc giữa hai mặt phẳng (SBC) và (SCD) bằng 60 0 .