Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A.
Ta có A(2;3;3); B(2;2;2)
Δ đi qua điểm A(2;3;3) và có vectơ chỉ phương A B → = 0 ; - 1 ; 1
Vậy phương trình của ∆ là x = 2 y = 3 - t z = 3 - t
Chọn A.
Gọi ∆ là đường thẳng cần tìm
Đường thẳng d có vecto chỉ phương a d → = 0 ; 1 ; 1
Ta có A(2;3;3); B(2;2;2)
∆ đi qua điểm A(2;3;3) và có vectơ chỉ phương 
Vậy phương trình của ∆ là
Chọn C.
*) Gọi A = d1 ∩ (α)
A ∈ d1 ⇒ A(2-a;1+3a;1+2a)
Mà điểm A thuộc mp(α) nên thay tọa độ điểm A vào phương trình mặt phẳng ta được
(2 - a) + 2(1 + 3a) – 3(1 + 2a) – 2= 0
2 – a + 2 + 6a – 3 – 6a – 2 = 0
⇒ a = -1 ⇒ A(3;-2;-1)
*) Gọi B = d2 ∩ (α)
B ∈ d2 ⇒ B(1-3b;-2+b;-1-b)
Mà điểm B thuộc mp(α) nên thay tọa độ điểm B vào phương trình mặt phẳng ta được:
(1 - 3b) + 2(-2 + b) - 3(-1 - b) - 2 = 0
1- 3b – 4 + 2b + 3 + 3b - 2 = 0
⇔ 2b - 2 = 0 ⇔ b = 1 ⇒ B(-2;-1;-2)
*) Đường thẳng d đi qua điểm A(3;-2;-1) và có vectơ chỉ phương 
Vậy phương trình chính tắc của d là x - 3 - 5 = y + 2 1 = z + 1 - 1
Đáp án D
HD: Để AB nhỏ nhất <=> AB là đoạn vuông góc chung của d, d'
Gọi A ∈ d => A(1+a;2-a;a) và B ∈ d => B(2b,1+b;2+b) ⇒ A B → = ( 2 b - a - 1 ; a + b - 1 ; b - a + 2 )
Vì A B ⊥ d A B ⊥ d ' ⇒ A B → . u d → A B → . u d ' → ⇔ 2 b - a - 1 - a - b + 1 + b - a + 2 = 0 2 ( 2 b - a - 1 ) + a + b - 1 + b - a + 2 = 0
⇔ - 3 a + 2 b + 2 = 0 - 2 a + 6 b - 1 = 0 ⇔ a = 1 b = 1 2
Vậy A(2;1;1), B 1 ; 3 2 ; 5 2 ⇒ A B → = - 1 ; 1 2 ; 3 2 = - 1 2 2 ; - 1 ; - 3
⇒ ( A B ) : x - 2 - 2 = y - 1 1 = z - 1 3
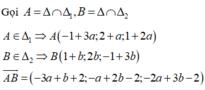
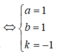
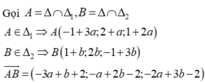
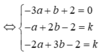
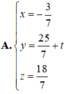
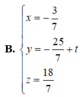
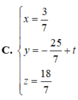
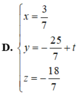
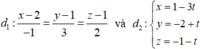
Chọn C
Gọi tọa độ giao điểm của đường thẳng ∆ và hai đường thẳng d và d’ lần lượt là A t ; - 4 + t ; - 13 + 2 t ; B - 7 + 3 t ' ; - 1 - 2 t ' ; 8 Tìm t và t’ từ điều kiện A B → cùng phương với véc tơ J → = 0 ; 1 ; 0 là véc tơ pháp tuyến của (oxz)