Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=2sinx + cosx +1. Tổng M2+ m2 có giá trị là
A. 18
B. 36
C. 12
D. 30
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
31 tháng 10 2018
Đúng(0)
Những câu hỏi liên quan
CM
13 tháng 1 2018
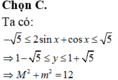
Đáp án A.
Điều kiện x ∈ ℝ
y = cos x + cos x − π 3 = cos x + cos x . cos π 3 + sin x . sin π 3 = cos x + 1 2 cos x + 3 2 sin x
= 3 2 cos x + 3 2 sin x
Cách 1: y = 3 3 2 cos x + 1 2 sin x = 3 sin x + π 3 Suy ra − 3 ≤ y ≤ 3
Vậy m = − 3 ; M = 3 và do đó M 2 + m 2 = 6
Cách 2:
Áp dụng bất đẳng thức Bunyakovsky ta có:
3 2 cos x + 3 2 sin x 2 ≤ 3 2 2 + 3 2 2 cos x 2 + sin x 2
⇔ 3 2 cos x + 3 2 sin x 2 ≤ 3 ⇔ − 3 ≤ y ≤ 3
⇒ M = 3 khi 2 3 cos x = 2 3 sin x 3 2 cos x + 3 2 sin x = 3
Tương tự ta có m = − 3 khi 2 3 cos x = 2 3 sin x 3 2 cos x + 3 2 sin x = − 3
⇒ M 2 + m 2 = 3 2 + − 3 2 = 6
Vậy ta chọn A.
CM
12 tháng 9 2019
Chọn C
Đặt 
Xét hàm 
trên đoạn [0;1] có 
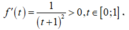
Suy ra hàm số đồng biến trên [0;1]
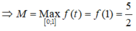và 
Khi đó, 
CM
9 tháng 12 2018
Đáp án A
Ta có: y = cos x + 2 sin x + 3 2 cos x − sin x + 4
⇒ y 2 cos x − sin x + 4 = cos x + 2 sin x + 3
⇔ 2 + y sin x + 1 − 2 y cos x = 4 y − 3 1
PT (1) có nghiệm ⇔ 2 + y 2 + 1 − 2 y 2 ≥ 4 y − 3 2
⇔ 11 y 2 − 24 y + 4 ≤ 0 ⇔ 2 11 ≤ y ≤ 2
Suy ra M = 2 m = 2 11 ⇒ M . m = 4 11
CM
27 tháng 1 2017
Đáp án D
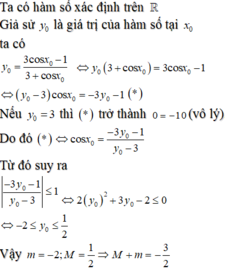
*Cách 2: Đặt ẩn phụ t = cos x đưa về hàm bậc nhất trên bậc nhất, rồi tìm min, max của hàm đó trên [-1;1]
CM
29 tháng 10 2019
Đáp án C
Phương pháp:
Biến đổi hàm số về hàm số bậc hai đối với cos x , đặt cos x = t và tìm GTLN, GTNN của hàm số với chú ý
Cách giải:
Ta có: y = 2 sin 2 x − cos x + 1
= 2 1 − cos 2 x − cos x + 1 = − 2 cos 2 x − cos x + 3
Đặt t = cos x − 1 ≤ t ≤ 1
y t = − 2 t 2 − t + 3 ⇒ y ' t = − 4 t − 1
y ' 0 = 0 ⇔ t = − 1 4 ∈ − 1 ; 1
⇒ M = max y = y − 1 4 = 25 8 ; m = min y = y 1 = 0 ⇒ M + m = 25 8
Chú ý khi giải:
HS thường nhầm lẫn khi tìm GTLN, GTNN của hàm số, hoặc ở bước đặt ẩn phụ quên không đặt điều kiện cho ẩn mới.
CM
31 tháng 10 2018
Chọn B
Hàm số xác định và liên tục trên đoạn [- 5 ; 5 ]
Ta có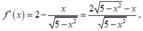 
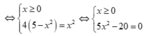
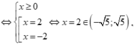
Ta có: 
Suy ra 
