Cho hàm số f x = e a x - 1 x k h i x ≠ 0 1 2 k h i x = 0 với a ≠ 0 . Tìm giá trị của a để hàm số f(x) liên tục tại x 0 = x
A. a = 1
B. a = 1 2
C. a = - 1
D. a = - 1 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: f(-2)=4+3=7
f(-1)=2+3=5
f(0)=3
f(1/2)=-1+3=2
f(-1/2)=1+3=4
b: g(-1)=1-1=0
f(0)=0-1=-1

Giải:
Bài 1: lần lượt thay các giá trị của x, ta có:
_Y=f(-1)= -5.(-1)-1=4
_Y=f(0)= -5.0-1=1
_Y=f(1)= -5.1-1=-6
_Y=f(1/2)= -5.1/2-1=-7/2
Bài 2:
Lần lượt thay các giá trị của x, ta có:
_Y=f(-2)=-2.(-2)+3=7
_Y=f(-1)=-2.(-1)+3=1
_Y=f(0)=-2.0+3=3
_Y=f(-1/2)=-2.(-1/2)+3=4
_Y=f(1/2)=-2.1/2+3=2

a: TXĐ: \(D=R\backslash\left\{-\dfrac{1}{2}\right\}\)
b: TXĐ: \(D=R\backslash\left\{-3;1\right\}\)
c: TXĐ: \(D=\left[-\dfrac{1}{2};3\right]\)

\(f'\left(x\right)=0\) có 3 nghiệm \(x=-1;0;2\)
Dấu của \(f'\left(x\right)\) trên trục số:
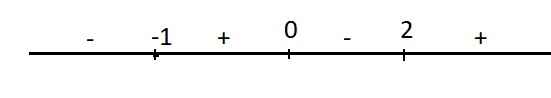
Ta thấy có 2 lần \(f'\left(x\right)\) đổi dấu từ âm sang dương nên hàm có 2 cực tiểu
Đáp án B
Ta có lim x → 0 f x = lim x → 0 e a x - 1 x = lim x → 0 e a x - 1 a x a = a vì lim x → 0 e a x - 1 a x = 1
Vậy để hàm số f(x) liên tục tại x 0 = x ⇔ lim x → 0 f x = f 0 ⇔ a = 1 2 .