Có hai lực vuông góc với nhau với các độ lớn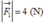 và
và 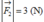 . Hợp lực của chúng tại với lực này các góc (lấy tròn tới độ).
. Hợp lực của chúng tại với lực này các góc (lấy tròn tới độ).
A. 30º và 60 °
B. 42º và 48º
C. 37º và 53 °
D. 35º và 45º
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
F 1 vuông góc với F 2
→ Góc hợp bởi hợp lực F với F 1 là
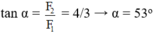
→ Góc hợp bởi hợp lực F với F2 là
β = 90 o - 53 o = 37 o

Chọn đáp án C
F1 vuông góc với F2
→ Góc hợp bởi hợp lực F với F1 là:
tan α = F2/F1 = 4/3 → α = 53o
→ Góc hợp bởi hợp lực F với F2 là:
β = 90o – 53o = 37o.

Hợp lực F có giới hạn:
\(\left|F_1-F_2\right|\le F\le\left|F_1+F_2\right|\)
\(\Leftrightarrow\left|10-15\right|\le F\le\left|10+15\right|\)
\(\Leftrightarrow5N\le F\le25N\)
\(\Rightarrow\) Chọn A, B, C

Đáp án D
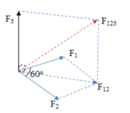
Hợp lực của F1 và F2 là:
F 12 = 2. F 1 . cos α 2 = 2.20. cos 30 0 = 20 3 N
F3 vuông góc với mp chứa F1 và F2 nên F3 vuông góc với F12.
Hợp lực của ba lực chính là hợp lực của F12 và F3.
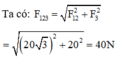

cùng chiều : F=F1+F2=7 N.
ngược chiều :F=|F1-F2|=1 N (Hợp lực ở đây có cùng chiều với F2).
tạo với nhau 1 góc 120 độ :F2=F12+F22+2*F1*F2*cos(120) = \(\sqrt{13}\) N.
Còn nếu muốn có gia tốc thì bạn phải cho khối lượng chứ .

a:
Gọi hai lực đồng quy đề bài cho lần lượt là \(\overrightarrow{F_1};\overrightarrow{F_2}\)
Gọi hợp lực của \(\overrightarrow{F_1};\overrightarrow{F_2}\) là \(\overrightarrow{F}\)
Do đó, ta có: \(\overrightarrow{F}=\overrightarrow{F_1}+\overrightarrow{F_2}\)
=>\(\left|\overrightarrow{F}\right|=\sqrt{F_1^2+F_2^2+2\cdot F_1\cdot F_2\cdot cos\left(\overrightarrow{F_1},\overrightarrow{F_2}\right)}\)
=>\(F=\sqrt{18^2+24^2+2\cdot18\cdot24\cdot cos25}\simeq41,02\left(N\right)\)
b: \(F=31N\)
=>\(\sqrt{F_1^2+F_2^2+2\cdot F_1\cdot F_2\cdot cos\left(\overrightarrow{F_1};\overrightarrow{F_2}\right)}=31\)
=>\(900+2\cdot18\cdot24\cdot cos\left(\overrightarrow{F_1};\overrightarrow{F_2}\right)=961\)
=>\(864\cdot cos\left(\overrightarrow{F_1};\overrightarrow{F_2}\right)=61\)
=>\(cos\left(\overrightarrow{F_1};\overrightarrow{F_2}\right)=\dfrac{61}{864}\)
=>\(\left(\overrightarrow{F_1};\overrightarrow{F_2}\right)\simeq86^0\)
Đáp án C