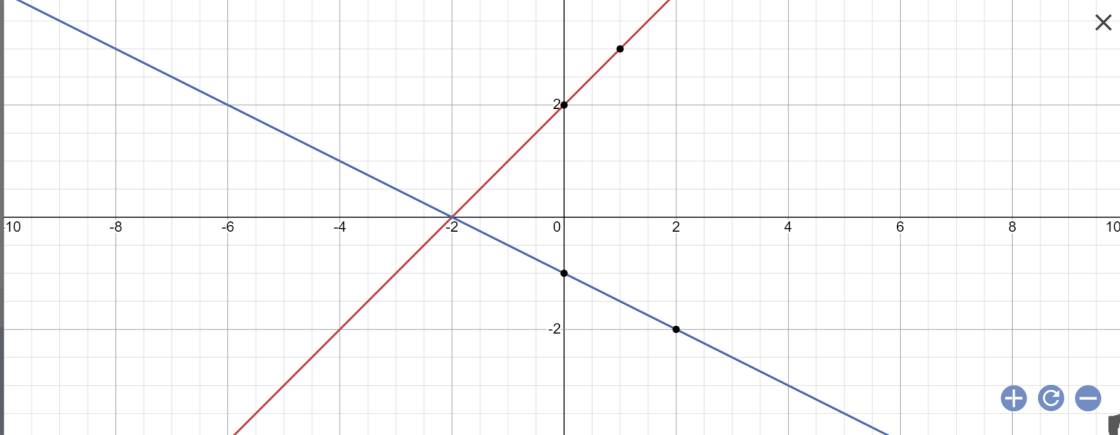
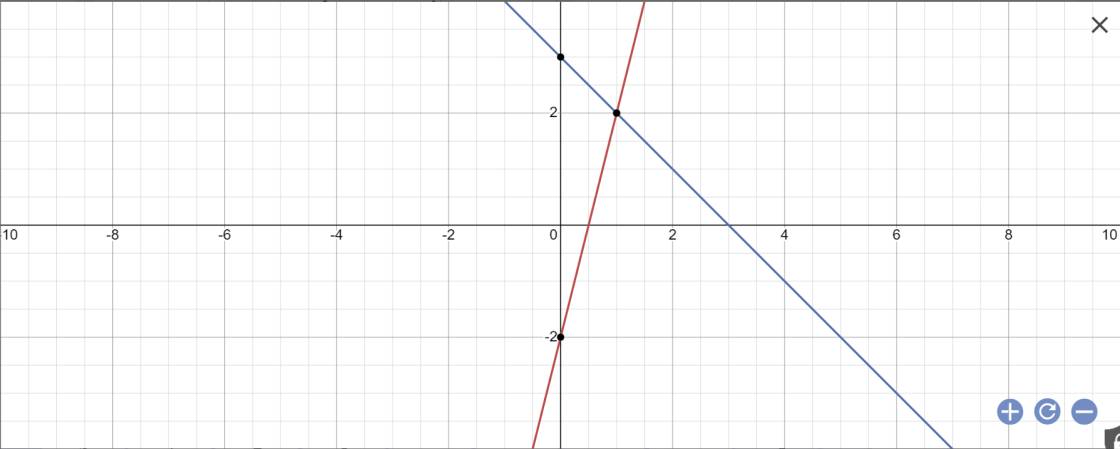
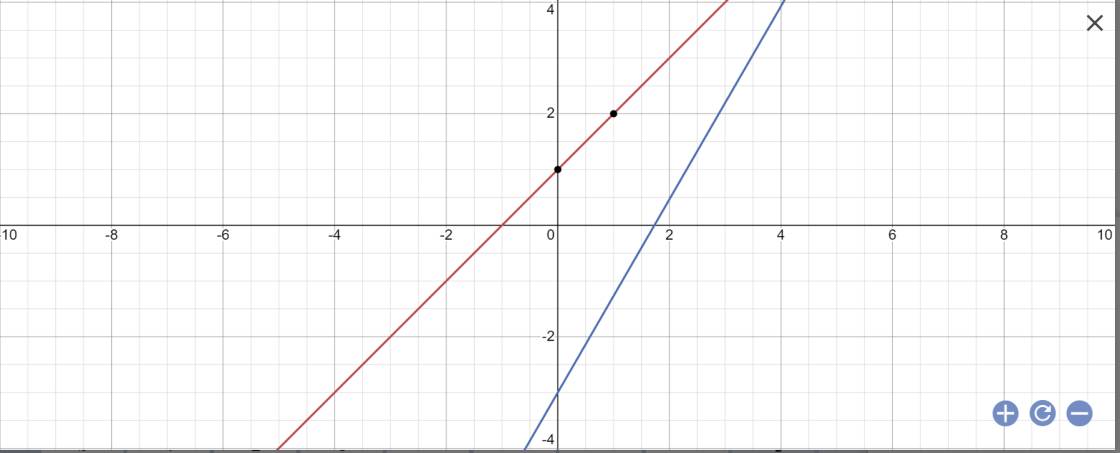
a) Vẽ các đường thẳng (d1) y=x-2 và (d2) y=-3\(y= -{3 \over 2}+3\) trên cùng một mặt phẳng tọa độ và chứng minh chúng cắt nhau tại điểm A trên trục hoành.
b) Gọi giao điểm của (d1) và (d2) với trục tung là B và C. Tính các góc của tam giác ABC.
c) Tính chu vi và diện tích của tam giác ABC.