Trong mặt phẳng Oxy, tập hợp các điểm M biểu diễn số phức z thỏa mãn điều kiện z - 4 i + z + 4 i = 10
A. Một đường tròn
B. Một elip
C. Một hypebol
D. Một parabol
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 8 2019
Chọn C.
Giả sử w = x + yi , khi đó ( 1) tương đương ( x - 7) 2+ ( y + 9) 2 ≤ 16
Suy ra tập hợp điểm biểu diễn số phức w là hình tròn tâm I(7; -9), bán kính r = 4
Vậy diện tích cần tìm là S = π.42 = 16π.
CM
26 tháng 10 2017
Chọn B.
Gọi M(x; y) là điểm biểu diễn của số phức z = x + yi trong mặt phẳng phức(x, y ∈ R).
Theo đề bài ta có
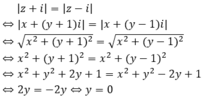
Vậy tập hợp các điểm M là đường thẳng y = 0 hay trục Ox
CM
6 tháng 1 2018
Đáp án A.
Gọi z = x ; y khi đó điều kiện trở thành:
x 2 + y − 1 2 = x 2 + y + 1 2 ⇔ y = − 1
Như vậy quỹ tích là một đường thẳng.
Đặt z = x + yi với x , y ∈ R
Từ giả thiết bài toán ta có
x + y i - 4 i + x + y i + 4 i = 10 ⇔ x + y - 4 i + x + y + 4 i = 10 ⇔ x 2 + y - 4 2 + x 2 + y + 4 2 = 10
Gọi F 1 0 ; - 4 , F 0 ; 4 . Khi đó M F 1 + M F 2 = 10
Vậy tập hợp các điểm M cần tìm là elip nhận F 1 F 2 = 8 làm tiêu cự, trục lớn bằng 10. Elip này có phương trình là x 2 9 + y 2 25 = 1
Đáp án B