Phân tích đa thức thành nhân tử:
a) 4 + xy - 2y;
b) x (x - y);
c) - 3x + 3y;
d)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

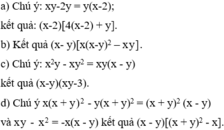

Lời giải:
a. Không phân tích được nữa
b. $x^2(x-y)+4(y-x)=x^2(x-y)-4(x-y)=(x-y)(x^2-4)=(x-y)(x-2)(x+2)$
c. $x^3+2x^2y+xy^2-4x=x(x^2+2xy+y^2-4)$
$=x[(x^2+2xy+y^2)-4]=x[(x+y)^2-2^2]=x(x+y-2)(x+y+2)$

`a)7x^3y^2+14x^2y^3+7xy^4`
`=7xy^2(x^2+2xy+y^2)`
`=7xy^2(x+y)^2`
______________________________________________
`b)x^2-xy+5x-5y`
`=x(x-y)+5(x-y)`
`=(x-y)(x+5)`
______________________________________________
`c)3x^2-6xy-12+3y^2`
`=3(x^2-2xy-4+y^2)`
`=3[(x-y)^2-4]`
`=3(x-y-2)(x-y+2)`
a)7x3y2+14x2y3+7xy4
=7xy2(x2+2xy+y2)
=7xy2(x+y)2
b)x2-xy + 5x - 5y
=x(x-y) + 5(x-y)
=(x-y) (x+5)

a: \(=\dfrac{2}{5}\left(xy-x-y^2+1\right)\)
\(=\dfrac{2}{5}\left[x\left(y-1\right)-\left(y-1\right)\left(y+1\right)\right]\)
\(=\dfrac{2}{5}\left(y-1\right)\left(x-y-1\right)\)
b: \(=x\left(x^2+2xy+y^2-9\right)\)
\(=x\left(x+y-3\right)\left(x+y+3\right)\)
a) =25(xy−x−y2+1)=25(xy−x−y2+1)
=25[x(y−1)−(y−1)(y+1)]=25[x(y−1)−(y−1)(y+1)]
=25(y−1)(x−y−1)=25(y−1)(x−y−1)
b) =x(x2+2xy+y2−9)=x(x2+2xy+y2−9)
=x(x+y−3)(x+y+3

a:=2(x-2)+y(x-2)
=(x-2)(y+2)
b: \(=\left(x+y\right)^2-4\)
=(x+y+2)(x+y-2)

a: \(=5a\left(x-2y\right)\)
b: \(=x\left(x-y\right)+\left(x-y\right)=\left(x-y\right)\left(x+1\right)\)
c: =(x-1)(x-7)
a)\(5ax-10ay=5a\left(x-2y\right)\)
b) \(x^2-xy+x-y=x\left(x-y\right)+\left(x-y\right)=\left(x+1\right)\left(x-y\right)\)
c) \(x^2-8x+7=\left(x-7\right)\left(x-1\right)\)

a: Ta có: \(2\left(x-1\right)^3-5\left(x-1\right)^2-\left(x-1\right)\)
\(=\left(x-1\right)\left[2\left(x-1\right)^2-5\left(x-1\right)-1\right]\)
\(=\left(x-1\right)\left(2x^2-4x+2-5x+5-1\right)\)
\(=\left(x-1\right)\left(2x^2-9x+6\right)\)
b: Ta có: \(x\left(y-x\right)^3-y\left(x-y\right)^2+xy\left(x-y\right)\)
\(=-x\left(x-y\right)^3-y\left(x-y\right)^2+xy\left(x-y\right)\)
\(=\left(x-y\right)\left[-x\left(x-y\right)^2-y\left(x-y\right)+xy\right]\)
\(=\left(x-y\right)\left[-x^3+2x^2y-xy^2-xy+y^2+xy\right]\)
\(=\left(x-y\right)\left(-x^3+2x^2y-xy^2+y^2\right)\)
a) \(2\left(x-1\right)^3-5\left(x-1\right)^2-\left(x-1\right)=\left(x-1\right)\left[2\left(x-1\right)^2-5\left(x-1\right)-1\right]=\left(x-1\right)\left(2x^2-4x+2-5x+5-1\right)=\left(x-1\right)\left(2x^2-9x+6\right)\)
b) \(x\left(y-x\right)^3-y\left(x-y\right)^2+xy\left(x-y\right)=\left(x-y\right)\left[-x\left(x-y\right)^2-y\left(x-y\right)+xy\right]=\left(x-y\right)\left(-x^3+2x^2y-xy^2-xy+y^2+xy\right)=\left(x-y\right)\left(-x^3+y^2+2x^2y-xy^2\right)\)
c) \(xy\left(x+y\right)-2x-2y=xy\left(x+y\right)-2\left(x+y\right)=\left(x+y\right)\left(xy-2\right)\)
d) \(x\left(x+y\right)^2-y\left(x+y\right)^2+y^2\left(x-y\right)=\left(x+y\right)^2\left(x-y\right)+y^2\left(x-y\right)=\left(x-y\right)\left(x^2+2xy+y^2+y^2\right)=\left(x-y\right)\left(x^2+2y^2+2xy\right)\)

\(a,=6x\left(x-2\right)-7\left(x-2\right)=\left(6x-7\right)\left(x-2\right)\)

a, \(x-2y+x^2-4y^2=\left(x-2y\right)+\left(x-2y\right)\left(x+2y\right)=\left(x-2y\right)\left(1+x+2y\right)\)
b, \(x^2-4x^2y^2+y^2+2xy=\left(x+y\right)^2-\left(2xy\right)^2\)
\(=\left(x+y-2xy\right)\left(x+y+2xy\right)\)
c, \(x^6-x^4+2x^3+2x^2=x^6+2x^3+1-x^4+2x^2-1\)
\(=\left(x^3+1\right)^2-\left(x^2-1\right)^2=\left(x^3-x^2+2\right)\left(x^3+x^2\right)\)
\(=x^2\left(x+1\right)\left(x^3-x^2+2\right)\)
d, \(x^3+3x^2+3x+1-8y^3=\left(x+1\right)^3-\left(2y\right)^3=\left(x+1-2y\right)\left(x+1+2y\right)\)
a) Ta có: \(x-2y+x^2-4y^2\)
\(=\left(x-2y\right)+\left(x-2y\right)\left(x+2y\right)\)
\(=\left(x-2y\right)\left(1+x+2y\right)\)
b: Ta có: \(x^2-4x^2y^2+y^2+2xy\)
\(=\left(x+y\right)^2-\left(2xy\right)^2\)
\(=\left(x+y-2xy\right)\left(x+y+2xy\right)\)

\(a,=x\left(x-8\right)\\ b,=x\left(x-y\right)-6\left(x-y\right)=\left(x-6\right)\left(x-y\right)\\ c,=\left(x-3\right)^2-y^2=\left(x-y-3\right)\left(x+y-3\right)\\ d,=\left(x+y\right)\left(x^2-xy+y^2\right)+2\left(x+y\right)\\ =\left(x+y\right)\left(x^2-xy+y^2+2\right)\)
a: \(x^2-8x=x\left(x-8\right)\)
c: \(x^2-6x+9-y^2=\left(x-3-y\right)\left(x-3+y\right)\)