Giúp mih phần trắc nghiệm vs 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
a: Xét ΔADC có
\(\dfrac{AM}{MD}=\dfrac{AP}{PC}\)
Do đó: MP//DC
Xét ΔCAB có
\(\dfrac{CQ}{QB}=\dfrac{CP}{PA}\)
Do đó: PQ//AB
hay PQ//CD
Xét ΔBCD có
\(\dfrac{BQ}{QC}=\dfrac{BN}{ND}\)
Do đó: NQ//DC
Ta có: PQ//CD
NQ//DC
mà PQ và NQ có điểm chung là Q
nên Q,P,N thẳng hàng(1)
Ta có: PQ//CD
PM//CD
mà PQ và PM có điểm chung là P
nên M,P,Q thẳng hàng(2)
Từ (1) và (2) suy ra M,N,P,Q thẳng hàng


Bài 17:
a) Xét tứ giác BDHF có
\(\widehat{BFH}\) và \(\widehat{BDH}\) là hai góc đối
\(\widehat{BFH}+\widehat{BDH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: BDHF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Bài 17:
b) Xét ΔABC có
AD là đường cao ứng với cạnh BC(gt)
CF là đường cao ứng với cạnh AB(gt)
AD cắt CF tại H(gt)
Do đó: H là trực tâm của ΔABC(Tính chất ba đường cao của tam giác)
Suy ra: BH\(\perp\)AC
hay BE\(\perp\)AC
Xét ΔFHB vuông tại F và ΔEHC vuông tại E có
\(\widehat{FHB}=\widehat{EHC}\)(hai góc đối đỉnh)
Do đó: ΔFHB\(\sim\)ΔEHC(g-g)
Suy ra: \(\dfrac{HF}{HE}=\dfrac{HB}{HC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(HB\cdot HE=HC\cdot HF\)(đpcm)

 giúp e vs ạ phần trắc nghiệm + bt ạ
giúp e vs ạ phần trắc nghiệm + bt ạ Các bạn giúp mình phần trắc nghiệm và tự luận nhé . Trắc nghiệm có một số câu ko đúng . Giúp mình nha
Các bạn giúp mình phần trắc nghiệm và tự luận nhé . Trắc nghiệm có một số câu ko đúng . Giúp mình nha giúp mk trắc nghiệm vs
giúp mk trắc nghiệm vs



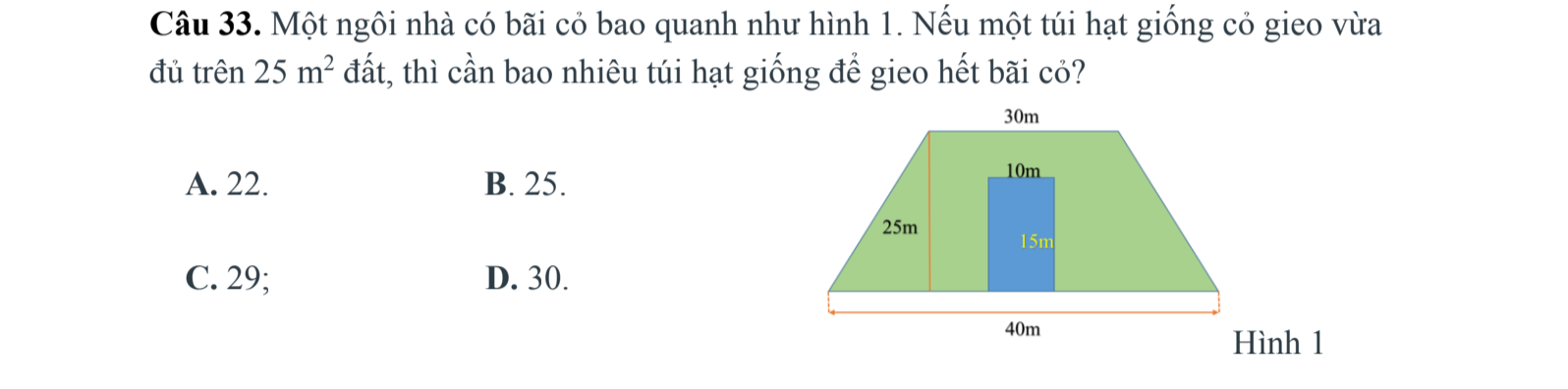
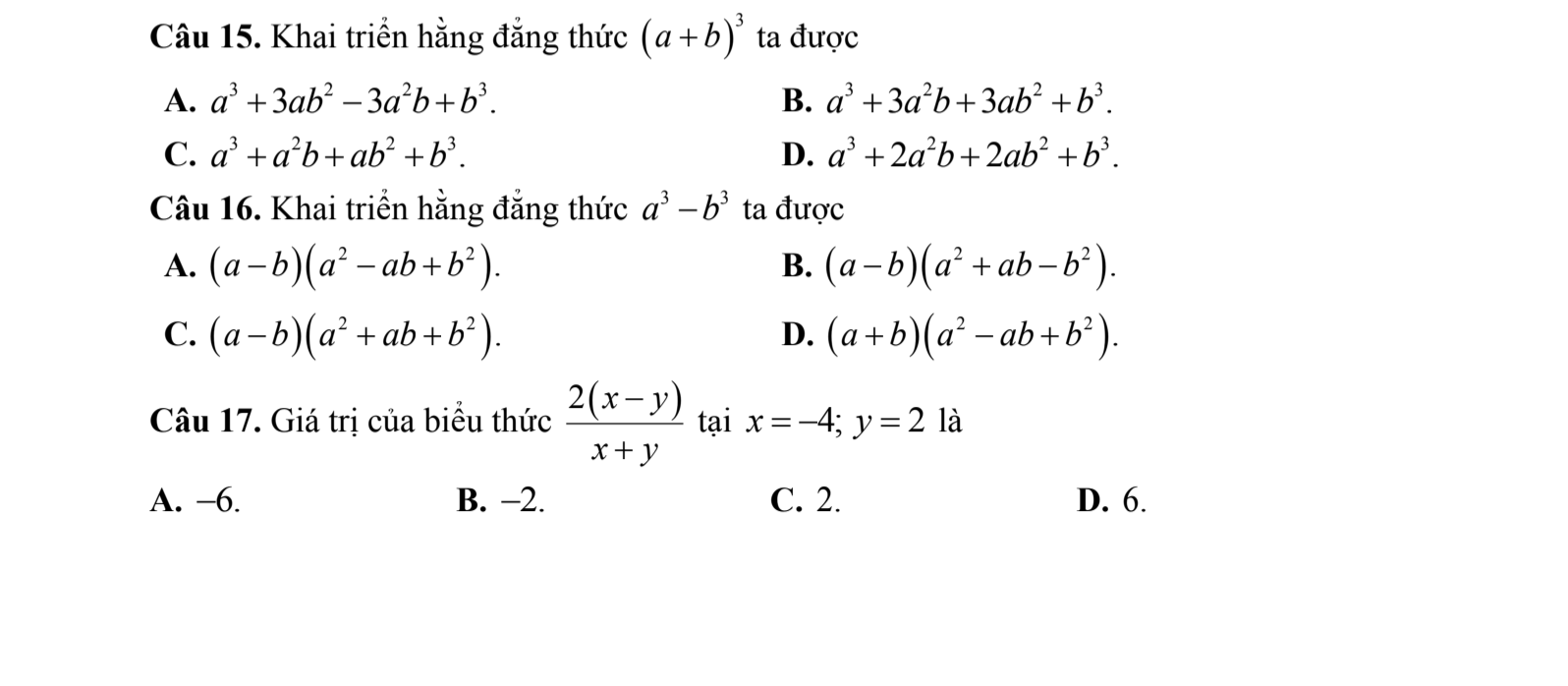


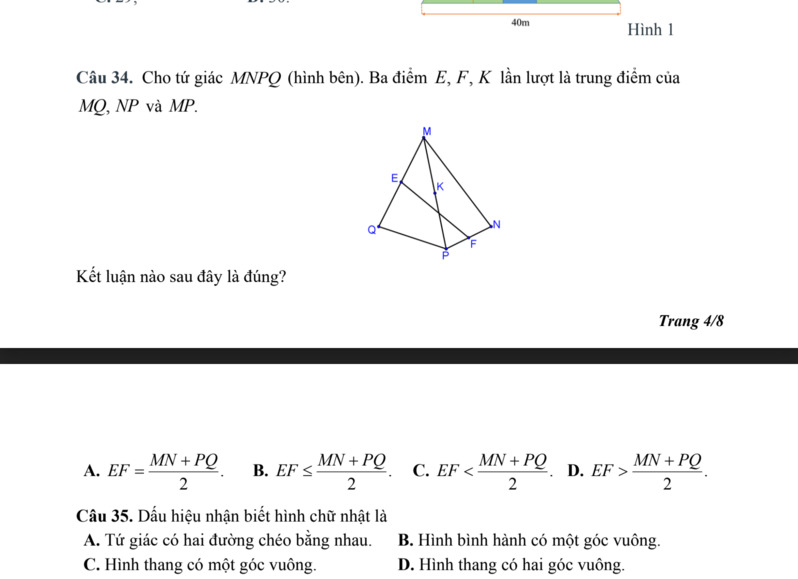

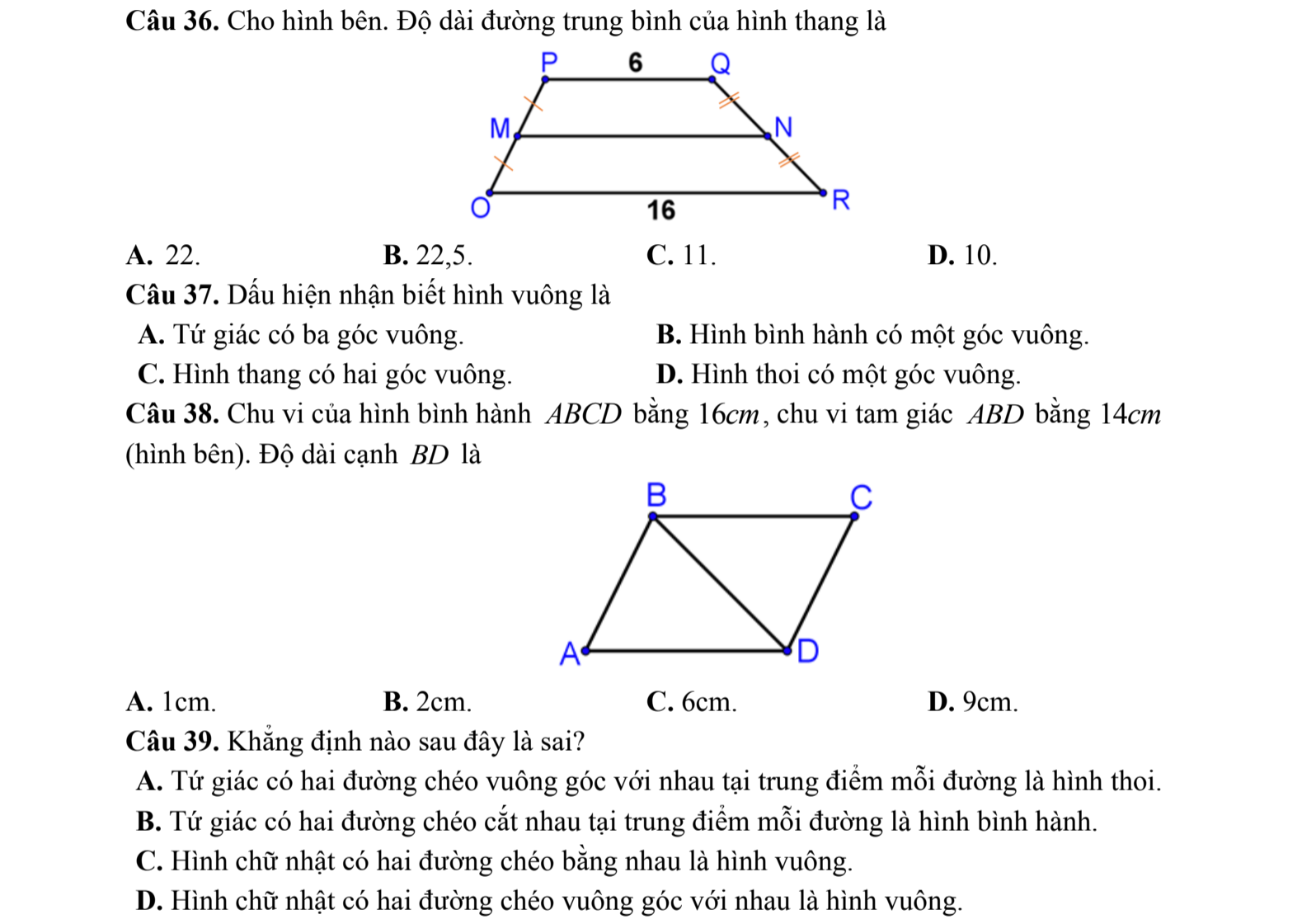


 Giúp em 45 câu trắc nghiệm này vs
Giúp em 45 câu trắc nghiệm này vs