Cho tam giác ABC có AB = AC = 3cm và A ^ = 120 0 . Tính độ dài đường tròn ngoại tiếp tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\)
=>\(\dfrac{3^2+3^2-BC^2}{2\cdot3\cdot3}=-\dfrac{1}{2}\)
=>18-BC^2=-9
=>BC^2=27
=>\(BC=3\sqrt{3}\left(cm\right)\)
\(\dfrac{BC}{sinA}=2R\)
=>\(2\cdot R=3\sqrt{3}:sin120=3\sqrt{3}:\dfrac{1}{2}=6\sqrt{3}\)
=>\(R=3\sqrt{3}\)

Xét ΔABC có \(BC^2=AB^2+AC^2\left(5^2=3^2+4^2\right)\)
nên ΔABC vuông tại A(Định lí Pytago đảo)
Ta có: I là tâm đường tròn ngoại tiếp ΔHAB(gt)
mà ΔHAB vuông tại H(gt)
nên I là trung điểm của AB
\(\Leftrightarrow AI=\dfrac{AB}{2}=\dfrac{3}{2}=1.5\left(cm\right)\)
Ta có: K là tâm đường tròn ngoại tiếp ΔHAC(gt)
mà ΔHAC vuông tại H(gt)
nên K là trung điểm của AC
\(\Leftrightarrow AK=\dfrac{AC}{2}=\dfrac{4}{2}=2\left(cm\right)\)
Áp dụng định lí Pytago vào ΔAKI vuông tại A, ta được:
\(AK^2+AI^2=IK^2\)
\(\Leftrightarrow KI^2=1.5^2+2^2=6.25\)
hay KI=2,5(cm)
Vậy: KI=2,5cm

Đặt AB = x ; AC = y ( ĐK x ; y > 0 )
BC = 2R = 2.5 = 10
Theo py ta go => x^2 + y^2 = BC^2 = 100
r = \(\frac{AB+AC-BC}{2}=\frac{x+y-10}{2}=3\Leftrightarrow x+y=16\) (2)
Từ (1) v/s (2) => x^2 + y^2 = 100
và x + y = 16

a, tam giác ABC vuông tại B có góc A = 30 độ => AC = 2 BC = 2. 3 = 6 cm
theo định lí Pytago ta có AB = \(\sqrt{ÃC^2-BC^2}=\sqrt{6^2-3^2}\) = \(3\sqrt{3}\) cm
góc C = 90 - 30 = 60 độ
b, tam giác ABH vuông tại H có góc A = 30 độ => AB = 2 BH => BH = \(\frac{3\sqrt{3}}{2}\)cm
theo định lí Pytago ta có AH = \(\sqrt{AB^2-BH^2}=\sqrt{\left(3\sqrt{3}\right)^2-\left(\frac{3\sqrt{3}}{2}\right)^2}=4,5cm\)
diện tích tam giác ABH =\(\frac{1}{2}.BH.AH=\frac{1}{2}.\frac{3\sqrt{3}}{2}.4,5=\frac{27\sqrt{3}}{8}\)cm vuông

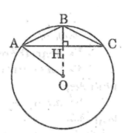

A ^ = 120 0 => O A C ^ = 60 0
=> ∆OAC đều => R = AC = 30cm
=> C = 2πR = 6π cm