Cho điểm A cách đường thẳng xy là 12 cm
a, Chứng minh (A; 13cm) cắt đường thẳng xy tại hai điểm phân biệt
b, Gọi hai giao điểm của (A; 13 cm) với xy là B, C. Tính độ dài đoạn thẳng BC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

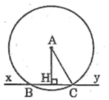
Kẻ AH ⊥ xy
Ta có: AH = 12cm
Bán kính đường tròn tâm I là 13cm nên R = 13cm
Mà AH = d = 12cm
Nên suy ra d < R
Vậy (A; 13cm) cắt đường thẳng xy tại hai điểm phân biệt B và C

Ta có : \(OC+OA=AC\)\(\Rightarrow OC=AC-OA=12-6=6\left(cm\right)\)
Vậy \(OA=OC\left(6cm=6cm\right)\)
hình(tự vẽ)
Ta có : Vì o nằm trên tia xy => hai tia ox và oy đối nhau mà c thuộc ox;a thuộc oy
=>o nằm giữa c và a =>ac=oc+oa thay ac=12cm và oa=6cm vào ta có:
=>12=oc+6
=>oc=12-6
=>oc=6(cm) mà có oa=6cm
=>oa=oc
=>đpcm

Vì O thuộc đường thẳng xy nên tia Ox và tia Oy đối nhau
mà A và B nằm ở hai nữa mặt phẳng đối nhau có bờ là đường thẳng xy (1)
và góc xOA = yOB (2)
Từ (1) và (2) suy ra xOA và yOB là hai góc đối đỉnh chung gốc O
Vì xOA và yOB là hai góc đối đỉnh nên tia OA và tia OB đối nhau ( vì tia Ox và Oy ở trên đã đối nhau rồi lên không cần nhắc lại )
Vì OA và OB đối nhau nên A ; O ; B thẳng hàng
Vậy A ; O ; B thẳng hàng
Nhớ k cho mình nhé! Thank you!!!

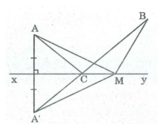
Vì A' đối xứng với A qua xy
⇒ xy là đường trung trực của AA'.
⇒ CA' = CA (t/chất đường trung trực)
MA' = MA (t/chất đường trung trực)
AC + CB = A'C + CB = A'B (1)
MA + MB = MA'+ MB (2)
Trong ∆ MA'B, ta có:
A'B < A'M + MB (bất đẳng thức tam giác) (3)
Từ (1), (2) và (3) suy ra: AC + CB < AM + MB

![[IMG]](http://d.f11.photo.zdn.vn/upload/original/2012/07/25/20/15/1343222151615470685_574_574.jpg)
+Gọi giao điểm của AC và BD là O\Rightarrow O là trung điểm của AC và BD
+Kẻ OO' vuông góc với xy
+Xét hình thang DD'BB' (DD'//BB')
Có O là trung điểm DB mà OO'//BB'
=> OO' là đường trung bình
=> 2OO'=DD'+BB'(*)
Xét ΔAA'C,có :OO'//AA',O là trung điểm của AC
=> OO' là đường trung bình
=> 2OO'=AA'(*) (*)
Từ (*) và (**) => đpcm
a, Kẻ OH vuông góc với xy thì OH =12cm <R do đó (O) cắt xy tại hai điểm B,C
b, Tìm được BC = 2, HC = 10cm