Cho tam giác ABC vuông tại B, AB = 9. Giá trị của A B → . A C → bằng
A.0
B.3
C.81
D.9
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 4 2019
Gọi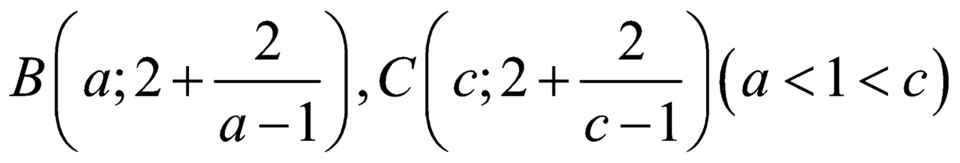 
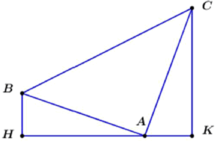
Gọi H, K lần lượt là hình chiếu của B, C trên trục 
vuông cân
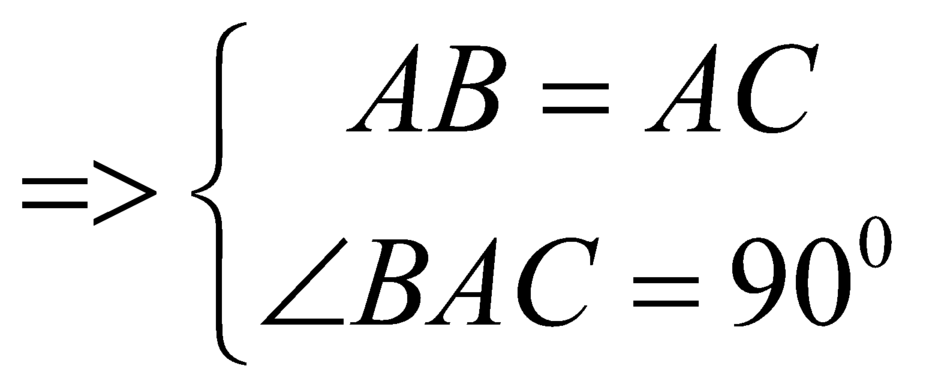
Ta có:
Mà:
Xét 
và 
ta có:
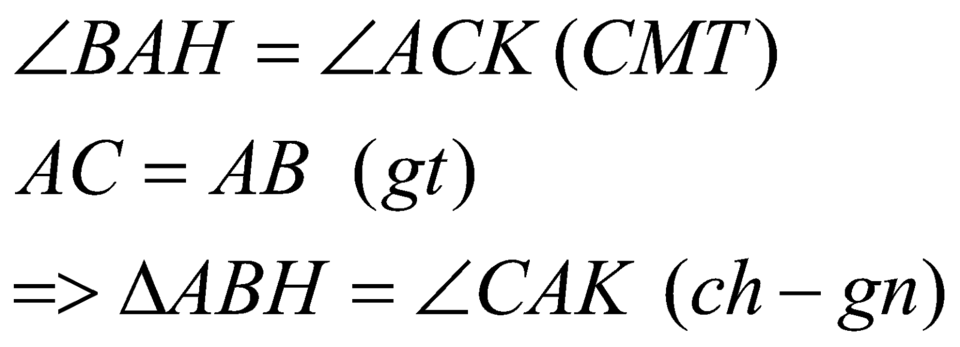
(các cạnh tương ứng bằng nhau)
Ta có:
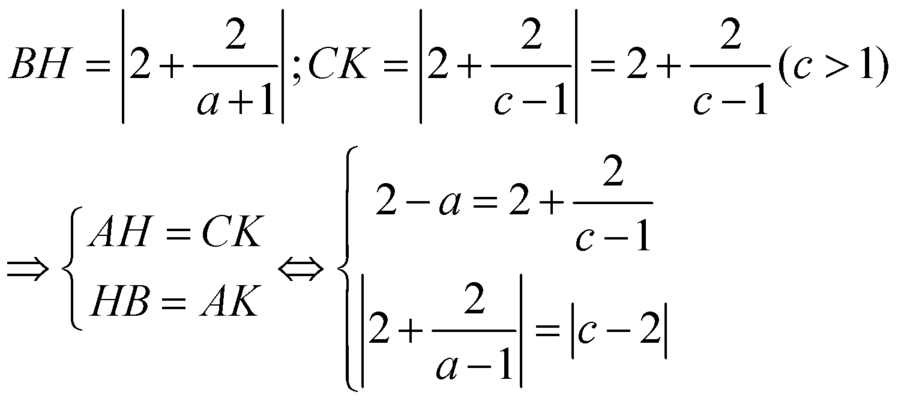
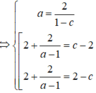
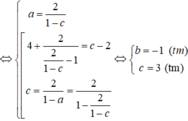
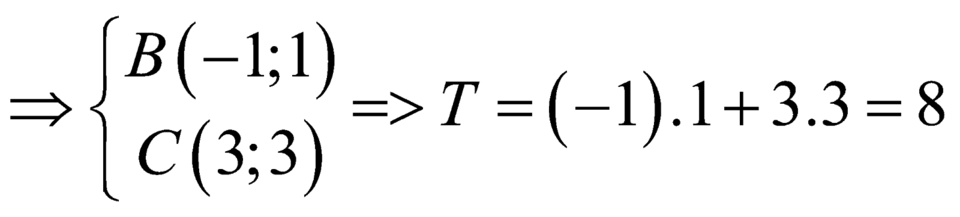
Chọn D.
CM
13 tháng 2 2017
Đáp án A
Ta có:
B A → = − 6 ; − 7 ; − 3
B C → = − m − 4 ; − m − 11 ; m + 7
Mặt khác: B A → . B C → = 0 nên m = − 4 .
8 tháng 3 2022
a: BC=15cm
b: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó:ΔBAD=ΔBHD
c: Xét ΔADK vuông tại A và ΔHDC vuông tại H có
DA=DH
\(\widehat{ADK}=\widehat{HDC}\)
Do đó:ΔADK=ΔHDC
Suy ra: DK=DC và AK=HC
d: Xét ΔBKC có BA/AK=BH/HC
nên AH//KC
29 tháng 10 2015
ta có
\(\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\)
\(a+b-2\sqrt{ab}\ge0\)
\(a+b\ge2\sqrt{ab}\)
\(\frac{a+b}{2}\ge\sqrt{ab}\)
25 tháng 12 2016
Ta có AH2=CH.BH=ab (1)
Gọi M là trung điểm của BC.
Xét tam giác AHM vuông tại H có AM là cạnh huyền --> AH\(\le\)AM (2)
Mà \(AM=\frac{BC}{2}=\frac{a+b}{2}\)(3)
Từ (1), (2) và (3) \(\Rightarrow a.b\le\frac{a+b}{2}\)
31 tháng 3 2019
CÂU 1:
a) \(2x+4+x^2=-2x+x-3x+2x\)
\(\Leftrightarrow2x+4+x^2=-2x\)
\(\Leftrightarrow x^2+4x+4=0\)
\(\Leftrightarrow\left(x+2\right)^2=0\)
\(\Leftrightarrow x+2=0\)
\(\Leftrightarrow x=-2\)
b) \(2x^2-5x-x=x^2+6x\)
\(\Leftrightarrow2x^2-5x-x-x^2-6x=0\)
\(\Leftrightarrow3x^2-12x=0\)
\(\Leftrightarrow3x\left(x-4\right)=0\)
Hoặc \(3x=0\Leftrightarrow x=0\)
Hoặc \(x-4=0\Leftrightarrow x=4\)
Ta có: tam giác ABC vuông tại B nên A B → ⊥ B C → ⇒ A B → . B C → = 0
A B → . A C → = A B → . ( A B → + B C → ) = A B → 2 + A B → . B C → = A B 2 + 0 = 81
Chọn C.