Trong mặt phẳng Oxy cho parabol (P) có phương trình: y = x 2 - 3 x + 1 . Phép đối xứng tâm I(4; -3) biến P thành (P’) có phương trình:
A. y = - x 2 + 13 x - 47
B. y = x 2 - 13 x + 47
C. y = - x 2 - 13 x - 47
D. y = - x 2 - 13 x + 47
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phép đối xứng trục Oy có:
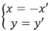
Thay vào phương trình (P) được y = 4 x ' 2 + 7 x ' + 3 hay y = 4 x 2 + 7 x + 3
Đáp án B

Phép đối xứng trục Ox có:
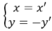
Thay vào phương trình (P) ta được: - y ' = 6 x ' 2 - 3 x ' + 13 hay y = - 6 x 2 + 3 x - 13
Đáp án C

Lấy M(x;y) thuộc d, phép đối xứng tâm I (x0; y0) biến M(x; y) thành M'(x'; y') thì
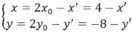
Thay vào phương trình d ta được :2(4 - x') - 6(-8 - y') + 5 = 0 ⇒ 2x' - 6y' - 61 = 0 hay 2x - 6y - 61 = 0.
Chọn đáp án B

Tâm đối xứng I thuộc d thì phép đối xứng tâm I biến d thành chính nó.
Nhận xét: lưu ý kiểm tra xem tâm có thuộc d không, cũng như với phép tịnh tiến thì kiểm tra xem vecto tịnh tiến có cùng phương với vecto chỉ phương của d không.
Đáp án B
Phép đối xứng tâm I biến M(x; y) thành M’(x’; y’) thì:
Thay vào phương trình (P) ta được:
- 6 - y ' = 8 - x ' 2 - 3 ( 8 - x ' ) + 1
⇒ - y ' = x ' 2 - 13 x ' + 47 hay
y = - x 2 + 13 x - 47
Đáp án A