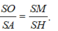II. Tự luận ( 4 điểm)
Tính bán kính của mặt cầu ngoại tiếp hình chóp tam giác đều S.ABC, biết các cạnh đáy có độ dài bằng a, cạnh bên S A = a 3 .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 8 2019
Chọn D.
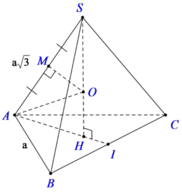
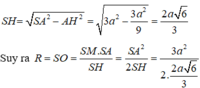
Gọi H là tâm của tam giác đều ABC, ta có SH⊥(ABC) nên SH là trục của tam giác ABC.
Gọi M là trung điểm của SA, trong mp (SAH) kẻ trung trực của SA cắt SH tại O thì OS = OA = OB = OC
Suy ra: O chính là tâm mặt cầu ngoại tiếp hình chóp S.ABC. Bán kính mặt cầu là R = SO.
Vì hai tam giác SMO và SHA đồng dạng nên ta có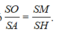 
Ta có:
CM
20 tháng 4 2019
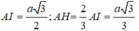
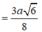
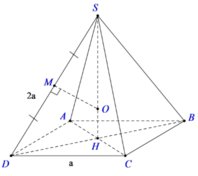
Cho hình chóp tứ giác đều S.ABCD.
Gọi H là tâm đáy thì SH là trục của hình vuông ABCD.
Gọi M là trung điểm của SD, trong mp (SDH) kẻ trung trực của đoạn SD cắt SH tại O. Suy ra; OS = OD (1)
Mà O thuộc trục SH của hình vuông ABCD nên:
OA = OB = OC = OD (2)
Từ (1) và (2) suy ra: OA = OB = OC= OD = OS
Do đó, O chính là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD. Bán kính mặt cầu là R = SO
Ta có:
CM
26 tháng 3 2019
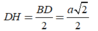
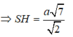
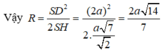
Đáp án B
Gọi H là trung điểm B C ⇒ A H ⊥ B C → S B C ⊥ A B C A H ⊥ S H .
Xét hai tam giác vuông SHA và BHA có H A chung S A = B A = a ⇒ Δ S H A = Δ B H A .
⇒ S H = B H = C H ⇒ Δ S B C vuông tại S ⇒ R b = B H = B C 2 .
Dễ thấy
G T = B C ⇒ R = R b 2 + R d 2 − G T 2 4 = B H 2 + R d 2 − B C 2 4 = R d = a
Xét tam giác ABC, có:
sin C = A B 2 R = 1 2 ⇒ cos C = 3 2 ⇒ B C = 2 H C = 2 A C . cos C = a 3
Trong tam giác vuông SBC, ta có S C = B C 2 − S B 2 = a 2 .
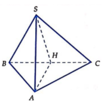
Gọi H là tâm của tam giác đều ABC.
Ta có SH ⊥ (ABC) nên SH là trục của tam giác ABC
Gọi M là trung điểm của SA, trong mp (SAH) kẻ trung trực của SA cắt SH tại O thì OS = OA (1)
Lại có, SH là trục của tam giác ABC và O ∈ SH nên: OA = OB = OC (2)
Từ (1) và (2) suy ra: OS = OA = OB = OC
Nên O chính là tâm mặt cầu ngoại tiếp hình chóp S.ABC.
Bán kính mặt cầu là R = SO.
Vì hai tam giác SMO và SHA đồng dạng nên ta có