Cho đường tròn tâm O , từ điểm A ở ngoài đường tròn kẻ hai tiếp tuyến AB AC , tới (O), B và C là tiếp điểm. Gọi giao điểm của đường thẳng AO và đường thẳng BC là H . a) Chứng minh 4 điểm A ,B, C, O cùng thuộc một đường tròn; b) Kẻ đường kính CE của (O) . Chứng minh AO //BE ; c) Kẻ OK vuông góc với AE tại K . Gọi I là giao điểm của hai đường thẳng BC và OK . Chứng minh OH .OA =OK .OI ; d) Chứng minh IE là tiếp tuyến của (O)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

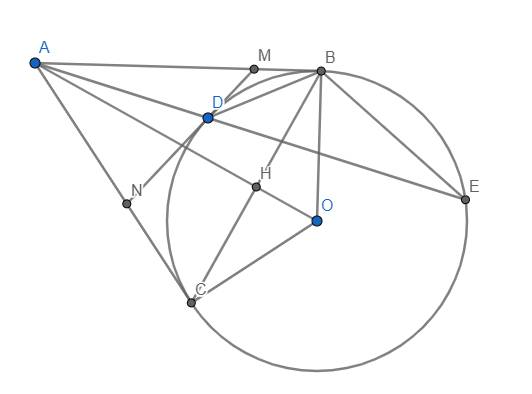
a) Do AB là tiếp tuyến của (O) tại B nên \(\widehat{ABO}=90^o\). CMTT, ta có \(\widehat{ACO}=90^o\) \(\Rightarrow\widehat{ABO}+\widehat{ACO}=180^o\) \(\Rightarrow\) Tứ giác ABOC nội tiếp (đpcm).
b) Theo tính chất 2 tiếp tuyến cắt nhau, ta có \(AO\perp BC\). Tam giác ABO vuông tại B, có đường cao BH nên \(AB^2=AH.AO\)
Mặt khác, lại có \(\widehat{ABD}=\widehat{ACB}\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung đó) nên \(\Delta ABD~\Delta AEB\left(g.g\right)\) \(\Rightarrow\dfrac{AB}{AE}=\dfrac{AD}{AB}\) \(\Rightarrow AB^2=AD.AE\)
Từ đó dễ dàng suy ra \(AD.AE=AH.AO\)
c) Do tính chất của 2 tiếp tuyến cắt nhau nên \(\left\{{}\begin{matrix}MD=MB\\ND=NC\end{matrix}\right.\)
Do đó \(C_{AMN}=AM+AN+MN\)
\(=AM+AN+\left(MD+ND\right)\)
\(=\left(AM+MD\right)+\left(AN+ND\right)\)
\(=\left(AM+MB\right)+\left(AN+NC\right)\)
\(=AB+AC\)
\(=2AB\)
Lại có \(AB=\sqrt{AO^2-R^2}=\sqrt{6^2-3,6^2}=4,8cm\)
\(\Rightarrow C_{AMN}=2AB=2.4,8=9,6cm\)

a, Ta có AC ; AB lần lượt là tiếp tuyến (O) với C;B là tiếp điểm
=> ^ACO = ^ABO = 900
Xét tứ giác ABOC có
^ACO + ^ABO = 1800
mà 2 góc này đối
Vậy tứ giác ABOC là tứ giác nt 1 đường tròn
hay các điểm A;B;O;C cùng thuộc 1 đường tròn
b, Ta có AB = AC ( tc tiếp tuyến cắt nhau )
OC = OB = R
Vậy OA là đường trung trực đoạn BC
=> OA vuông BC
Xét tam giác ACO vuông tại C, đường cao CH
Ta có AC^2 = AH.AO ( hệ thức lượng )
Xét tam giác ACE và tam giác ADC
^A _ chung
^ACE = ^ADC ( cùng chắn cung CE )
Vậy tam giác ACE ~ tam giác ADC (g.g)
\(\dfrac{AC}{AD}=\dfrac{AE}{AC}\Rightarrow AC^2=AE.AD\)
=> AH . AO = AE . AD (*)
Xét tam giác AHE và tam giác ADO ta có
AH/AD = AE/AO ( tỉ lệ thức * )
^A _ chung
Vậy tam giác AHE ~ tam giác ADO (g.g)
=> ^AHE = ^ADO (1)
Lại có ^ACE = ^CDE ( cùng chắn cung CE ) (2)
Lấy (1) + (2) ta được ^BDC = ^AHE + ^ACE
dm có ông nào giải hộ tôi điiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii


a, A,H,O thẳng hàng vì AH,AO cùng vuông góc với BC
HS tự chứng minh A,B,C,O cùng thuộc đường tròn đường kính OA
b, Ta có K D C ^ = A O D ^ (cùng phụ với góc O B C ^ )
=> ∆KDC:∆COA (g.g) => AC.CD = CK.AO
c, Ta có: M B A ^ = 90 0 - O B M ^ và M B C ^ = 90 0 - O M B ^
Mà O M B ^ = O B M ^ (∆OBM cân) => M B A ^ = M B C ^
=> MB là phân giác A B C ^ . Mặt khác AM là phân giác B A C ^
Từ đó suy ra M là tâm đường tròn nội tiếp tam giác ABC
d, Kẻ CD ∩ AC = P. Chứng minh ∆ACP cân tại A
=> CA = AB = AP => A là trung điểm CK

a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC


a) Hai tam giác vuông ABO và ACO có chung cạnh huyền AO nên A, B, O, C cùng thuộc đường tròn đường kính AO.
Vậy tứ giác ABOC là tứ giác nội tiếp.
b) Ta thấy ngay \(\Delta ABD\sim\Delta AEB\left(g-g\right)\)
\(\Rightarrow\frac{AB}{AE}=\frac{AD}{AB}\Rightarrow AE.AD=AB^2\)
Xét tam giác vuông ABO có BH là đường cao nên áp dụng hệ thức lượng ta có:
\(AH.AO=AB^2\)
Suy ra AD.AE = AH.AO
c) Ta có \(\widehat{PIK}+\widehat{IKQ}+\widehat{P}+\widehat{Q}=360^o\)
\(\Rightarrow2\left(\widehat{PIO}+\widehat{P}+\widehat{OKQ}\right)=360^o\)
\(\Rightarrow\widehat{PIO}+\widehat{P}+\widehat{OKQ}=180^o\)
Mặt khác \(\widehat{PIO}+\widehat{P}+\widehat{IOP}=180^o\)
\(\Rightarrow\widehat{IOP}=\widehat{OKQ}\Rightarrow\Delta PIO\sim\Delta QOK\)
\(\Rightarrow\frac{IP}{PO}=\frac{OQ}{KQ}\Rightarrow PI.KQ=PO^2\)
Sử dụng bất đẳng thức Cô-si ta có:
\(IP+KQ\ge2\sqrt{IP.KQ}=2\sqrt{OP^2}=PQ\)
acje cho hỏi 2 tam giác đồng dạng ở câu b là góc nào í chỉ ro rõ cho e với ạk

a: Xét (O) có
AB,AC là tiếp tuyến
nên AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc BC và H là trung điểm của BC
b: Xét (O) co
ΔBDC nội tiếp
BD là đường kính
=>ΔBCD vuông tại C
=>DC//OA

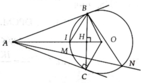
a, A B M ^ = A N B ^ = 1 2 s đ B M ⏜
Chứng minh được: ∆ABM:∆ANB (g.g) => ĐPCM
b, Chứng minh AO ^ BC áp dụng hệ thức lượng trong tam giác vuông ABO và sử dụng kết quả câu a) Þ AB2 = AH.AO
c, Chứng minh được A B I ^ = C B I ^ B I ⏜ = C I ⏜ => BI là phân giác A B C ^ . Mà AO là tia phân giác B A C ^ => I là tâm đường tròn nội tiếp ∆ABC
a: Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
Do đó: OBAC là tứ giác nội tiếp