Một công ti có 85 xe chở khách gồm hai loại, xe chở được 4 khách và xe chở được 7 khách. Dùng tất cả số xe đó, tối đa công ti chở một lần được 445 khách. Hỏi công ti đó có mấy xe mỗi loại?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 1 2018
Gọi xe 4 chỗ là a, số xe 7 chỗ là b:
\(\hept{\begin{cases}a+b=5\\4a+7b=445\end{cases}}\Leftrightarrow\hept{\begin{cases}a=75\\b=50\end{cases}}\)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
29 tháng 1 2018
Gọi số xe chở 4 khách là x
Gọi số xe chở 7 khách là y
Ta có hệ phương trình
x+y=85 (1)
4x+7y=445 (2)
Gải hệ phương trình trên để tính số xe mỗi loại
CM
8 tháng 1 2019
Gọi x là số xe chở được 45 khách, y là số xe chở được 12 khách. Ta có hệ phương trình
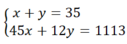
Nếu dùng máy tính cầm tay, ta nhập hệ phương trình vào máy, sẽ cho ngay kết quả là phương án C.
Nếu không dùng máy tính, ta có thể xét các phương án, với nhận xét là số xe 45 chỗ càng nhiều thì tổng số khách trở được càng lớn. Bắt đầu từ phương án A vì có số xe 45 chỗ là 20 dễ tính nhẩm, ta được tổng số khách chở được là 1080, ít hơn số 1113, nên phương án A bị loại. Các phương án B và D có số xe 45 chỗ ít hơn 20 nên số khách chở được càng ít hơn, nên B và D cũng bị loại.
Đáp án: C
21 tháng 7 2017
Chở hết số khách là: 100-13 = 87 khách
Đặt số xe chở 4 người là x, số xe chở 7 người là y
=> x+y = 15 xe, 4x + 7y = 87 người
=> (4x+7y) - 4(x+y) = 87 - 4.15 = 27
=> 4x+7y - 4x - 4y = 27
=> 3y = 27
=> y = 9
=> x = 15- y = 15 - 9 = 6
Vậy số loại chở 4 người là 6 xe, số loại chở 7 người là 9 xe
21 tháng 7 2017
số khách xe đã chỡ được:100-13=87ng
gọi số xe chở 4ng:x số xe chở 7ng:y
x+y=15xe 4x + 7y=87ng
4x *(15-y) + 7y =87 mình nói thêm mình sẽ bỏ 'x' ở bốn thay bằng (15-y)nhé
4 *(15-y) + 7y =87
4 * 15 - 4*y + 7y =87
60 - 4*y + 7y =87
60 + 3y = 87
3y = 87 - 60
3y =27
y =27 : 3
y=9
x=15-y=15-9=6
vậy số xe chở 4 ng :6xe số xe chở 7ng:9xe nhớ nha nếu đúng
BT
4 tháng 5 2017
Gọi số xe chở được 4 khách là: \(x\left(x\in N,x>0\right)\)
số xe chở được 7 khách là: \(y\left(y\in N,y>0\right)\).
Do tổng số xe là 85 xe nên: \(x+y=85\).
Dùng tất cả số xe đó, tối đa công ty chở được 445 khách nên: \(4x+7y=445\)
Theo bài ra ta có phương trình:
\(\left\{{}\begin{matrix}x+y=85\\4x+7y=445\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=50\left(tm\right)\\y=35\left(tm\right)\end{matrix}\right.\)
Vậy số xe chở được 4 khách là: 50 xe, số xe chở được 7 khách là 35 xe.
Gọi x là số xe 4 chỗ, y là số xe 7 chỗ. Điều kiện x và y nguyên dương.
Ta có hệ phương trình.
thỏa mãn điều kiện của bài toán).
Vậy công ty có 50 xe 4 chỗ và 35 xe 7 chỗ.