Cho x O y ^ = 120 ° , điểm A thuộc tia phân giác của góc xOy. Kẻ A B ⊥ O x ( B ∈ O x ) và A C ⊥ O y / ( C ∈ O y ) . Tam giác ABC là tam giác gì? Tại sao?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Xét 2 tam giác vuông AOC và AOB, ta có :
+ Góc COA bằng góc BOA ( vì OA là tia phân giác của góc xOy )
+ OA là cạnh huyền chung
=> Tam giác AOC bằng AOB ( CH_GN ) => CA = CB ( 2 cạnh tương ứng ) => CAB là tam giác cân tại A
- Trong tam giác cân CAB ta có góc CAB bằng 60 độ ( Vì góc CAO bằng 180 độ trừ cho tổng hai góc AOC + OCA hay nói cách khác là góc CAO = 180 - ( 60 + 90 ) = 30
+ Mà góc CAO bằng góc BAO => góc BAO bằng 30 độ
+ Có ( góc ) CAO + BAO = CAB = 60 độ )
- Vì CAB là tam giác cân có một góc bằng 60 độ suy ra tam giác CAB là tam giác đều

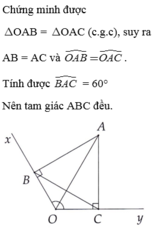
Ta có hình vẽ:
Xét tam giác OAC và tam giác OAB có:
góc COA = góc BOA (OA là phân giác góc O)
OA: cạnh chung
góc B = góc C = 900
(đây là trường hợp cạnh huyền góc nhọn)
=> tam giác OAC = tam giác OAB (g.c.g)
=> AC = AB (2 cạnh tương ứng)
Vì AC = AB nên \(\Delta\)ABC là tam giác cân

ko biết có đúng ko nhưng bn vào đây nhé: /hoi-dap/question/54769.html