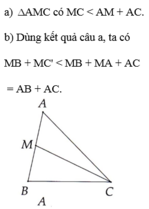
Tam giác ABC, điểm M thuộc cạnh AB.
a) So sánh MC với AM + AC.
b) Chứng minh MB + MC < AB + AC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A B C M
a) trong một tam giác thì tổng độ dài 2 cạnh bát kì luôn lớn hơn cạnh còn lại nên
tam giác AMC có AM + AC > CM
b) vì M thuộc cạnh AB nên AM + MB = AB
ta có: \(AB+AC=AM+MB+AC=\left(AM+AC\right)+MB\)
mà \(AM+AC>MC\)(cmt) \(\Rightarrow AB+AC=\left(AM+AC\right)+MB>MC+MB\)
vậy \(AB+AC>MC+MB\)
BVì M thuộc trong tam giác ABC nên tia BM thuộc trong B , nó cắt AC Tại D
D nằm giữa A và C, M nằm giữa B và D
Trong Tam giác BAD có
BM + MD < BA + AD + DCTRong tam giác MDC có MC - MD < DC
Cộng 2 vế của 1 và 2 với nhau ta được : BM +MC
CÒn phần sau mình chưa làm xin lỗi bạn

a) Xét Tam giác AMC. Áp dụng BĐT trong tam giác ta được: MC<AM+AC
b) Ta có: MC<AM+AC
Cộng cả 2 vế với MB: MB+MC<MB+AM+AC
mà MB+MC=AB
=> MB+MC<AB+AC
Học tốt

BVì M thuộc trong tam giác ABC nên tia BM thuộc trong B , nó cắt AC Tại D
D nằm giữa A và C, M nằm giữa B và D
Trong Tam giác BAD có
BM + MD < BA + AD + DC
TRong tam giác MDC có MC - MD < DC
Cộng 2 vế của 1 và 2 với nhau ta được : BM +MC
CÒn phần sau mình chưa làm xin lỗi bạn

a) Xét ΔBMC ta có: MB + MC > BC (bất đẳng thức tam giác)
b)
*Xét ΔABM ta có: AM + BM > AB (1)
*Xét ΔACM ta có: AM + CM > AC (2)
*Xét ΔBMC ta có: BM + CM > BC (3)
Từ (1); (2); (3)
=> AM + BM + AM + CM + BM + CM > AB + AC + BC
=> 2. AM + 2. BM + 2. CM > AB + AC + BC
=> 2. (AM + BM + CM) > AB + AC + BC
Hay: 2. (MA + MB + MC) > AB + BC + CA
c)Gọi I là giao điểm của BM và AC.
Áp dụng bất đẳng thức tam giác vào ΔIMC ta có: MC<MI+IC (1)
Cộng MB vào hai vế (1) ta được: MC+MB<MI+IC+MB
⇒MC+MB<MI+MB+IC
⇒MC+MB<IB+IC (2)
d)Áp dụng bất đẳng thức tam giác vào ΔIBA ta có: IB<IA+AB (3)
Cộng IC vào hai vế (3) ta được: IB+IC<IA+AB+IC
⇒ IB+IC<IA+IC+AB
⇒IB+IC<AC+AB (4)
e)Từ (2) và (4) suy ra MB+MC<AB+AC
f)Áp dụng bđt tam giác, ta có:
AB+AI > BI = MB+MI, CI + MI > MC
=> AB + AI + CI + MI > MB + MI + MC
Mà AI + CI = AC
=> AB + AC > MB + MC [1]
Áp dụng bđt tam giác, ta cũng có:
BA + BC > MA + MC [2],
CA + CB > MA + MB [3]
Từ [1][2][3] => 2 (AB+AC+CA) > MA + MB + MC
=> MA + MB + MC < AB + AC + BC (đpcm)

a) Xét ΔBMC ta có: MB + MC > BC (bất đẳng thức tam giác)
b)
*Xét ΔABM ta có: AM + BM > AB (1)
*Xét ΔACM ta có: AM + CM > AC (2)
*Xét ΔBMC ta có: BM + CM > BC (3)
Từ (1); (2); (3)
=> AM + BM + AM + CM + BM + CM > AB + AC + BC
=> 2. AM + 2. BM + 2. CM > AB + AC + BC
=> 2. (AM + BM + CM) > AB + AC + BC
Hay: 2. (MA + MB + MC) > AB + BC + CA
c)Gọi I là giao điểm của BM và AC.
Áp dụng bất đẳng thức tam giác vào ΔIMC ta có: MC<MI+IC (1)
Cộng MB vào hai vế (1) ta được: MC+MB<MI+IC+MB
⇒MC+MB<MI+MB+IC
⇒MC+MB<IB+IC (2)
d)Áp dụng bất đẳng thức tam giác vào ΔIBA ta có: IB<IA+AB (3)
Cộng IC vào hai vế (3) ta được: IB+IC<IA+AB+IC
⇒ IB+IC<IA+IC+AB
⇒IB+IC<AC+AB (4)
e)Từ (2) và (4) suy ra MB+MC<AB+AC
f)Áp dụng bđt tam giác, ta có:
AB+AI > BI = MB+MI, CI + MI > MC
=> AB + AI + CI + MI > MB + MI + MC
Mà AI + CI = AC
=> AB + AC > MB + MC [1]
Áp dụng bđt tam giác, ta cũng có:
BA + BC > MA + MC [2],
CA + CB > MA + MB [3]
Từ [1][2][3] => 2 (AB+AC+CA) > MA + MB + MC
=> MA + MB + MC < AB + AC + BC (đpcm)

a, Vì \(BC^2=400=256+144=AC^2+AB^2\) nên tam giác ABC vuông tại A
b, Áp dụng HTL: \(AM=\dfrac{AB\cdot AC}{BC}=9,6\left(cm\right)\)
\(BM=\dfrac{AB^2}{BC}=7,2 \left(cm\right)\)
c, Áp dụng HTL: \(AE\cdot AB=AM^2\)
Áp dụng PTG: \(AM^2=AC^2-MC^2\)
Vậy \(AE\cdot AB=AC^2-MC^2\)
d, Áp dụng HTL: \(AE\cdot AB=MB\cdot MC=AM^2\)
\(\left\{{}\begin{matrix}\widehat{EAM}=\widehat{ACM}\left(cùng.phụ.\widehat{MAC}\right)\\\widehat{AEM}=\widehat{AMC}=90^0\end{matrix}\right.\Rightarrow\Delta AEM\sim\Delta CMA\left(g.g\right)\\ \Rightarrow EM\cdot AC=AM^2\)
Vậy ta được đpcm