CÁC GIÚP MÌNH GIẢI TOÁN NÀY NHÉ !
BÀI 1 GIẢI PHƯƠNG TRÌNH
a ) X4 _ 4X3 _ 19X2 + 106X _ 120 = 0
b) 4X4 + 12X3 + 5X2 _ 6X _ 15 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 1 2022
\(a,x^4-4x^3-19x^2+106x-120=0\\ \Rightarrow\left(x-4\right)\left(x^3-19x+30\right)=0\Rightarrow\left(x-4\right)\left(x+5\right)\left(x^2-5x+6\right)=0\\ \Rightarrow\left(x-4\right)\left(x+5\right)\left(x-2\right)\left(x-3\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=4\\x=-5\\x=2\\x=3\end{matrix}\right.\)
Vậy pt có tập nghiệm \(S=\left\{-5;2;3;4\right\}\)
\(b,4x^4+12x^3+5x^2-6x-15=0\\ \Rightarrow\left(x-1\right)\left(4x^3+16x^2+21x+15\right)=0\\ \Rightarrow\left(x-1\right)\left[\left(4x^3+10x^2\right)+\left(6x^2+15x\right)+\left(6x+15\right)\right]=0\\ \Rightarrow\left(x-1\right)\left[2x^2\left(2x+5\right)+3x\left(2x+5\right)+3\left(2x+5\right)\right]=0\\ \Rightarrow\left(x-1\right)\left(2x+5\right)\left(2x^2+3x+3\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{5}{2}\\2x^2+3x+3=0\left(vô.lí\right)\end{matrix}\right.\)
Vậy pt có tập nghiệm \(S=\left\{1;-\dfrac{5}{2}\right\}\)
LD
3
12 tháng 2 2022
a: =>7x=63
hay x=9
b: =>3x=-15
hay x=-5
d: =>-6x=-16
hay x=8/3
12 tháng 2 2022
a) \(7x=63\Leftrightarrow x=9\)
b) \(3x=-15\Leftrightarrow x=-5\)
c) \(2x-5=0\Leftrightarrow2x=5\Leftrightarrow x=\dfrac{5}{2}\)
d) \(-6x=-16\Leftrightarrow x=\dfrac{8}{3}\)
AH
Akai Haruma
Giáo viên
5 tháng 3 2021
Lời giải:
a) $0,2x^2+0,4x-7=0$
$\Leftrightarrow 2x^2+4x-70=0$
$\Leftrightarrow x^2+2x-35=0$
$\Leftrightarrow (x-5)(x+7)=0$
$\Rightarrow x=5$ hoặc $x=-7$
b)
$\frac{1}{2}x^2+11x+60,5=0$
$\Leftrightarrow x^2+22x+121=0$
$\Leftrightarrow (x+11)^2=0\Leftrightarrow x=-11$
c)
$5x^2+\sqrt{3}-1=0$
$\Leftrightarrow 5x^2=1-\sqrt{3}< 0$ (vô lý)
Vậy PT vô nghiệm.
DT
Đỗ Thanh Hải
CTVVIP
16 tháng 4 2021
1) \(\left\{{}\begin{matrix}2x+y=10\\5x-3y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}10x+5y=50\\10x-6y=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}11y=44\\2x+y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=4\\x=3\end{matrix}\right.\)
Vậy hpt có nghiệm (x;y) = (3;4)
2)
a) 3x2 - 2x - 1 = 0
\(\Leftrightarrow3x^2-3x+x-1=0\)
\(\Leftrightarrow3x\left(x-1\right)+\left(x-1\right)=0\)
\(\Leftrightarrow\left(3x+1\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=1\end{matrix}\right.\)
Vậy pt có nghiệm x = 1 hoặc x = 3
b) Đặt x2 = t (t \(\ge\) 0)
Pt trở thành: t2 - 20t + 4 = 0
\(\Delta\) = (-20)2 - 4.1.4 = 400 - 16 = 384
=> pt có 2 nghiệm phân biệt t1 = \(\dfrac{20+8\sqrt{6}}{2}=10+4\sqrt{6}\)
t2 = \(\dfrac{20-8\sqrt{6}}{2}=10-4\sqrt{6}\)
=> x1 = \(\sqrt{10+4\sqrt{6}}=\sqrt{\left(2+\sqrt{6}\right)^2}=2+\sqrt{6}\)
x2 = \(2-\sqrt{6}\)
CM
23 tháng 7 2019
a) x 4 – 5 x 2 + 4 = 0 ( 1 )
Đặt x 2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : t 2 – 5 t + 4 = 0 ( 2 )
Giải (2) : Có a = 1 ; b = -5 ; c = 4 ⇒ a + b + c = 0
⇒ Phương trình có hai nghiệm t 1 = 1 ; t 2 = c / a = 4
Cả hai giá trị đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x 2 = 1 ⇒ x = 1 hoặc x = -1;
+ Với t = 4 ⇒ x 2 = 4 ⇒ x = 2 hoặc x = -2.
Vậy phương trình (1) có tập nghiệm S = {-2 ; -1 ; 1 ; 2}.
b) 2 x 4 – 3 x 2 – 2 = 0 ; ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 2 t 2 – 3 t – 2 = 0 ( 2 )
Giải (2) : Có a = 2 ; b = -3 ; c = -2
⇒ Δ = ( - 3 ) 2 - 4 . 2 . ( - 2 ) = 25 > 0
⇒ Phương trình có hai nghiệm
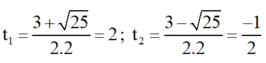
Chỉ có giá trị t 1 = 2 thỏa mãn điều kiện.
+ Với t = 2 ⇒ x 2 = 2 ⇒ x = √2 hoặc x = -√2;
Vậy phương trình (1) có tập nghiệm S = {-√2 ; √2}.
c) 3 x 4 + 10 x 2 + 3 = 0 ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 3 t 2 + 10 t + 3 = 0 ( 2 )
Giải (2) : Có a = 3; b' = 5; c = 3
⇒ Δ ’ = 5 2 – 3 . 3 = 16 > 0
⇒ Phương trình có hai nghiệm phân biệt
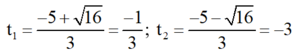
Cả hai giá trị đều không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.
8 tháng 8 2021
c) Ta có: \(C=4x^2+y^2-4xy+8x-4y+4\)
\(=\left(2x-y\right)^2+2\cdot\left(2x-y\right)\cdot2+2^2\)
\(=\left(2x-y+2\right)^2\)
LT
15 tháng 4 2021
a) \(\left\{{}\begin{matrix}2x+3y=-5\\6x-5y=27\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}6x+9y=-15\\6x-5y=27\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}14y=-42\\2x+3y=-5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=-3\\2x+3.\left(-3\right)=-5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=-3\\2x-9=-5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=-3\\2x=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=-3\\x=2\end{matrix}\right.\)
Vậy phương trình có nghiệm là: \(\left\{{}\begin{matrix}y=-3\\x=2\end{matrix}\right.\)
b) \(3x^2+4x=0\)
\(\Leftrightarrow x\left(3x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\3x+4=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{4}{3}\end{matrix}\right.\)
Vậy phương trình có tập nghiệm là: \(S=\left\{0;-\dfrac{4}{3}\right\}\)
c) Đặt: \(x^2=t\left(t\ge0\right)\)
\(\Rightarrow\) Ta có phương trình mới:
\(t^2-3t-4=0\)
Ta có: a - b + c = 1 + 3 - 4 = 0
\(\Rightarrow t_1=-1\left(loại\right);t_2=4\left(TM\right)\)
\(\Rightarrow x=\pm2\)
Vậy tập nghiệm của phương trình là: S = {2; -2}
15 tháng 4 2021
a, \(\left\{{}\begin{matrix}2x+3y=-5\\6x-5y=27\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x+9y=-15\left(1\right)\\6x-5y=27\left(2\right)\end{matrix}\right.\)
Lấy (1) - (2) ta được : \(14y=-15-27=-42\Leftrightarrow y=-3\)
\(\Rightarrow6x-27=-15\Leftrightarrow6x=12\Leftrightarrow x=2\)
Vậy \(\left(x;y\right)=\left(2;-3\right)\)
b, \(3x^2+4x=0\Leftrightarrow x\left(3x+4\right)=0\Leftrightarrow x=0;x=-\dfrac{4}{3}\)
c, \(x^4-3x^2-4=0\Leftrightarrow x^4+x^2-4x^2-4=0\)
\(\Leftrightarrow x^2\left(x^2-4\right)+x^2-4=0\Leftrightarrow\left(x^2+1\right)\left(x-2\right)\left(x+2\right)=0\)
\(\Leftrightarrow x=\pm2;x^2+1>0\)
Vậy nghiệm của phương trình là x = -2 ; x = 2
KT
6 tháng 2 2018
c) \(\left(x+1\right)\left(x+2\right)\left(x+4\right)\left(x+5\right)=40\)
\(\Leftrightarrow\)\(\left(x^2+6x+5\right)\left(x^2+6x+8\right)-40=0\)
Đặt \(x^2+6x+5=t\) ta có:
\(t\left(t+3\right)-40=0\)
\(\Leftrightarrow\)\(t^2+3t-40=0\)
\(\Leftrightarrow\)\(\left(t-5\right)\left(t+8\right)=0\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}t-5=0\\t+8=0\end{cases}}\)
Thay trở lại ta có: \(\orbr{\begin{cases}x^2+6x=0\\x^2+6x+13=0\end{cases}}\)
(*) \(x^2+6x=0\)
\(\Leftrightarrow\)\(x\left(x+6\right)=0\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}x=0\\x+6=0\end{cases}}\)\(\Leftrightarrow\)\(\orbr{\begin{cases}x=0\\x=-6\end{cases}}\)
(*) \(x^2+6x+13=0\)
\(\Leftrightarrow\)\(\left(x+3\right)^2+4=0\) (vô lý)
Vậy......
PT
1
CM
18 tháng 4 2019
a) 4 x 4 + x 2 − 5 = 0
Đặt x 2 = t (t ≥ 0). Phương trình trở thành:
4 t 2 + t − 5 = 0
Nhận thấy phương trình có dạng a + b + c = 0 nên phương trình có nghiệm
t 1 = 1 ; t 2 = ( − 5 ) / 4
Do t ≥ 0 nên t = 1 thỏa mãn điều kiện
Với t = 1, ta có: x 2 = 1 ⇔ x = ± 1
Vậy phương trình có 2 nghiệm x 1 = 1 ; x 2 = − 1
b) 3 x 4 + 4 x 2 + 1 = 0
Đặt x 2 = t ( t ≥ 0 ) . Phương trình trở thành:
3 t 2 + 4 t + 1 = 0
Nhận thấy phương trình có dạng a - b + c = 0 nên phương trình có nghiệm
t 1 = - 1 ; t 2 = ( - 1 ) / 3
Cả 2 nghiệm của phương trình đều không thỏa mãn điều kiện t ≥ 0
Vậy phương trình đã cho vô nghiệm.
thiếu, làm tiếp nek
=>(x-3)(x3-x2-22x+40)=0
=>x-3=0
x3-x2-22x+40=0
=>x=3
x=4;x=-5
a. => x4-3x3-x3+3x2-22x2+66x+40x-120 =0
=>x3(x-3)-x2(x-3)-22x(x-3)+40(x-3)=0
=>(x-3)(x3-x2-22x+40