Tìm x,y thuộc Z biết:
a, (x-3)(2y + 1) = 7
b, (2x + 1)(3y - 2) = -55
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MH
13 tháng 10 2021
\(\dfrac{x}{-3}=\dfrac{y}{5}\)⇒\(\dfrac{x}{-6}=\dfrac{y}{10}\)
\(\dfrac{y}{2}=\dfrac{z}{7}\)⇒\(\dfrac{y}{10}=\dfrac{z}{35}\)
⇒\(\dfrac{x}{-6}=\dfrac{y}{10}=\dfrac{z}{35}\)
⇒\(\dfrac{2x}{-12}=\dfrac{3y}{30}=\dfrac{z}{35}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{2x}{-12}=\dfrac{3y}{30}=\dfrac{z}{35}=\dfrac{2x-3y+z}{-12-30+35}=\dfrac{42}{-7}=-6\)
⇒\(\left\{{}\begin{matrix}x=-6.-6=36\\y=-6.10=-60\\z=-6.35=-210\end{matrix}\right.\)
13 tháng 10 2021
\(a,\dfrac{x}{-3}=\dfrac{y}{5}\Rightarrow\dfrac{x}{-6}=\dfrac{y}{10};\dfrac{y}{2}=\dfrac{z}{7}\Rightarrow\dfrac{y}{10}=\dfrac{z}{35}\\ \Rightarrow\dfrac{x}{-6}=\dfrac{y}{10}=\dfrac{z}{35}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{-6}=\dfrac{y}{10}=\dfrac{z}{35}=\dfrac{2x}{-12}=\dfrac{3y}{30}=\dfrac{2x-3y+z}{-12-30+35}=\dfrac{42}{-7}=-6\\ \Rightarrow\left\{{}\begin{matrix}x=36\\y=-60\\z=-210\end{matrix}\right.\)
\(b,6x=4y=z\Rightarrow\dfrac{6x}{12}=\dfrac{4y}{12}=\dfrac{z}{12}\Rightarrow\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{12}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{12}=\dfrac{2x}{4}=\dfrac{3y}{9}=\dfrac{2x-3y+z}{4-9+12}=\dfrac{42}{7}=6\\ \Rightarrow\left\{{}\begin{matrix}x=12\\y=18\\z=72\end{matrix}\right.\)
\(c,x=-2y\Rightarrow\dfrac{x}{-2}=y\Rightarrow\dfrac{x}{-4}=\dfrac{y}{2}\\ 7y=2z\Rightarrow\dfrac{y}{2}=\dfrac{z}{7}\\ \Rightarrow\dfrac{x}{-4}=\dfrac{y}{2}=\dfrac{z}{7}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{-4}=\dfrac{y}{2}=\dfrac{z}{7}=\dfrac{2x}{-8}=\dfrac{3y}{6}=\dfrac{2x-3y+z}{-8+6+7}=\dfrac{42}{5}\\ \Rightarrow\left\{{}\begin{matrix}x=-\dfrac{168}{5}\\y=\dfrac{84}{5}\\z=\dfrac{294}{5}\end{matrix}\right.\)
CM
4 tháng 5 2019
a) ( 2 x + 1 ) ( 3 y − 2 ) = − 55
Suy ra ( 2 x + 1 ) v à ( 3 y − 2 ) ∈ Ư ( - 55 ) = 1 ; − 1 ; 5 ; − 5 ; 11 ; − 11 ; 55 ; − 55
Khi đó ta có bảng sau:
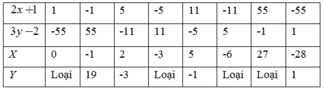
b) ( x − 3 ) ( 2 y + 1 ) = 7
Suy ra ( x − 3 ) và ( 2 y + 1 ) ∈ Ư ( 7 ) = 1 ; − 1 ; 7 ; − 7
Khi đó ta có bảng sau
c) y ( y 4 + 12 ) = − 5
Suy ra ( y 4 + 12 ) ∈ Ư ( - 5 ) = 1 ; − 1 ; 5 ; − 5
Vì y 4 ≥ 0 ⇒ y 4 + 12 ≥ 12 ⇒ không có giá trị của y thỏa mãn ycbt.
H
1
7 tháng 2 2022
a) \(\left(x+1\right)\left(y+4\right)=7\).
-Vì \(x,y\in Z\) nên ta có thể viết:
\(\left(x+1\right)\left(y+4\right)=1.7\) hay \(\left(x+1\right)\left(y+4\right)=7.1\) hay \(\left(x+1\right)\left(y+4\right)=\left(-1\right).\left(-7\right)\) hay \(\left(x+1\right)\left(y+4\right)=\left(-7\right).\left(-1\right)\)
+Xét trường hợp \(\left(x+1\right)\left(y+4\right)=1.7\):
\(\Rightarrow x+1=1\) và \(y+4=7\)
\(\Rightarrow x=0\left(tmđk\right)\) và \(y=3\left(tmđk\right)\).
+Xét trường hợp \(\left(x+1\right)\left(y+4\right)=7.1\):
\(\Rightarrow x+1=7\) và \(y+4=1\)
\(\Rightarrow x=6\left(tmđk\right)\) và \(y=-3\left(tmđk\right)\).
+Xét trường hợp \(\left(x+1\right)\left(y+4\right)=\left(-1\right).\left(-7\right)\):
\(\Rightarrow x+1=-1\) và \(y+4=-7\)
\(\Rightarrow x=-2\left(tmđk\right)\) và \(y=-11\left(tmđk\right)\).
+Xét trường hợp \(\left(x+1\right)\left(y+4\right)=\left(-7\right).\left(-1\right)\):
\(\Rightarrow x+1=-7\) và \(y+4=-1\)
\(\Rightarrow x=-8\left(tmđk\right)\) và \(y=-5\left(tmđk\right)\).
b) \(xy+2x-3y=-1\)
\(\Rightarrow xy+2x-3y+1=0\)
\(\Rightarrow y\left(x-3\right)=-2x-1\)
\(\Rightarrow y=-\dfrac{2x+1}{x-3}=\dfrac{2\left(x-3\right)-5}{x-3}=2-\dfrac{5}{x-3}\)
-Vì \(y\in Z\) \(\Rightarrow5⋮\left(x-3\right)\).
\(\Rightarrow\left(x-3\right)\inƯ\left(5\right)\)
\(\Rightarrow x-3\in\left\{1;-1;5;-5\right\}\)
\(\Rightarrow x\in\left\{4;2;8;-2\right\}\) (đều thỏa mãn điều kiện).
+Với \(x=4\) thì \(y=\dfrac{5}{4-3}=5\) (tmđk).
+Với \(x=2\) thì \(y=\dfrac{5}{2-3}=-5\) (tmđk).
+Với \(x=8\) thì \(y=\dfrac{5}{8-3}=1\) (tmđk)
+Với \(x=-2\) thì \(y=\dfrac{5}{-2-3}=-1\) (tmđk).
NT
0
KK
1
6 tháng 2 2018
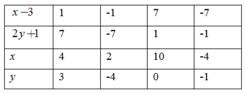
a) Do (x-3).(2y+1)=7
nên (x-3),(2y+1) thuộc Ư(7)
mà Ư(7)={1;-1;7;-7}
mà 2y+1 là số nguyên lẻ
nên x-3 thuộc {1;-1;7;-7}
2y+1 thuộc {7;-7;1;-1}
nên x thuộc {4;2;10;-4}
2y thuộc {6;-8;0;-2}= y thuộc {3;-4;0;-1}
12 tháng 10 2021
Bài 2:
a: \(3x^2-3xy=3x\left(x-y\right)\)
b: \(x^2-4y^2=\left(x-2y\right)\left(x+2y\right)\)
c: \(3x-3y+xy-y^2=\left(x-y\right)\left(3+y\right)\)
d: \(x^2-y^2+2y-1=\left(x-y+1\right)\left(x+y-1\right)\)
NT
0
29 tháng 11 2016
b. - 55 = - 5 x 11 = 5 x (-11)
Xét 4 TH:
1, 2x + 1 = -5
3y - 2 = 11
và 2, 2x + 1 = 5
3y - 2 = 11
Và ngược lại. Giải là xong bạn nhé!
29 tháng 11 2016
a. (x - 3) . (2y + 1) = 7
(x - 3) . (2y + 1) = 1.7 = (-1).(-7)
Cứ cho x - 3 = 1 => x = 4
2y + 1 = 7 => y = 3
Tiếp x - 3 = 7 => x = 10
2y + 1 = 1 => y = 0
x-3 = -1 ...