Tập xác định của hàm số y = 2 tanx – 3cot x là
A. R
K
Khách
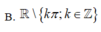
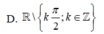
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 9 2018
Đáp án là B
• Hàm số y = sin x ; y = cos x có tập xác định D = ℝ .
• Hàm số y = tan x & y = cot x có tập xác định lần lượt D = ℝ \ π 2 + k π ; D = ℝ \ k π .
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 6 2021
1.
ĐKXĐ: \(\left\{{}\begin{matrix}cosx\ne0\\tanx-sinx\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}cosx\ne0\\\dfrac{sinx}{cosx}-sinx\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}cosx\ne0\\sinx\ne0\\cosx\ne1\end{matrix}\right.\) \(\Leftrightarrow sin2x\ne0\Leftrightarrow x\ne\dfrac{k\pi}{2}\)
2.
ĐKXĐ: \(sin2x\ne0\Leftrightarrow x\ne\dfrac{k\pi}{2}\)
3.
ĐKXĐ: \(\left\{{}\begin{matrix}sin\left(x-\dfrac{\pi}{4}\right)\ne0\\cos\left(x-\dfrac{\pi}{4}\right)\ne0\end{matrix}\right.\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{2}\right)\ne0\Leftrightarrow cos2x\ne0\)
\(\Leftrightarrow x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
18 tháng 12 2020
Câu 1. Hàm số xác định \(\Leftrightarrow\cos x\ne0\Leftrightarrow x\ne\dfrac{\pi}{2}+k2\pi\)
Câu 2. có \(-1\le\sin3x\le1\Leftrightarrow2\le\sin3x+3\le4\)
tập giá trị của hàm số : [2;4]
CM
9 tháng 3 2018
Đáp án B
Điều kiện: cos x ≠ 0 ⇔ x ≠ π 2 + k π ⇒
TXĐ: D = ℝ \ π 2 + k π , k ∈ ℤ
CM
14 tháng 8 2017
Đáp án B
Hàm số xác định khi và chỉ khi cos x ≠ 0 ⇔ x ≠ π 2 + π 2 π , k ∈ ℤ
CM
29 tháng 8 2018
Đáp án A
Hàm số xác định c osx ≠ 0
⇔ x ≠ π 2 + k π , k ∈ ℤ ⇒ D = ℝ \ π 2 + k π , k ∈ ℤ .
PT
1
CM
11 tháng 9 2017
Đáp án D
Tìm điều kiện xác định của hàm số:
- P x Q x xác định nếu Q x ≠ 0.
- P x xác định nếu P x ≥ 0.
- tan u x xác định nếu u x ≠ k π , cot u x xác định nếu x ≠ π 2 + k π
Hàm số xác định khi: cos x ≠ 0 sin x ≠ 0 ⇔ x ≠ k π x ≠ π 2 + k π ⇔ x ≠ k π 2 .
Vậy TXĐ của hàm số là D = ℝ \ k π 2 , k ∈ ℤ .
Đáp án D