Cho tứ diện đều S.ABC. Gọi I là trung điểm của AB, M là một điểm lưu động trên đoạn AI. Qua M vẽ mặt phẳng (∝) //(SIC). Khi đó thiết diện của mặt phẳng (∝) và tứ diện S.ABC là:
A. tam giác cân tại M
B. tam giác đều
C. hình bình hành
D. hình thoi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
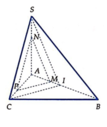
Trong A B C kẻ M P / / C I P ∈ A C . Trong S A C kẻ P N / / S C N ∈ S A .
⇒ M N P / / S I C ⇒ M N P ≡ α
Suy ra thiết diện giữa α và tứ diện S.ABC là tam giác MNP.
Do S.ABC là tứ diện đều nên ta đặt S A = S B = S C = S D = A B = B C = C A = 2 x
⇒ A I = x ; C I = 2 x 3 2 = x 3
Ta có M P / / C I ⇒ M P C I = A P A C = A M A I = a x ⇒ M P = a x . x 3 = a 3
Tương tự ta có M N = a 3 .
Ta có N P S C = A P A C = a x ⇒ N P = a x . S C = a x .2 x = 2 a .
Chu vi tam giác MNP là C = 2 a + a 3 + a 3 = 2 a 1 + 3 . Ta chọn B.

Đáp án A
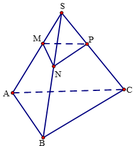
Gọi N, P là hai điểm lần lượt thuộc S B , S C thỏa mãn M N / / A B , M P / / A C .
Ta có M N // A B ⇒ M N // A B C M P // A C ⇒ M P // A B C ⇒ M N P / / A B C .
Gọi h 1 là đường cao của ΔMNP ứng với đáy MN.
Gọi h 2 là đường cao của ΔABC ứng với đáy AB.
Dễ thầy ΔMNP đồng dạng ΔABC ta có M N A B = h 1 h 2 = k .
Vậy để thỏa mãn yêu cầu bài toán
S Δ M N P S Δ A B C = 1 2 h 1 . M N 1 2 h 2 . A B = 1 2 ⇔ k . k = 1 2 ⇔ k = 2 2

Đáp án B

Trong (ABC), kẻ đường thẳng d đi qua M song song CI
d cắt AC tại H
Trong (SAB) kẻ đường thẳng x đi qua M và song song SI
X cắt SA tại J
⇒ (MHJ) là thiết diện cần tìm
Gọi tứ diện đều cạnh 2a ⇒ AI = a
Ta có AM = x và M J S I = A M A I (MJ // SI theo cách dựng)
A M A I = M H C I (MH // CI theo cách dựng)
J H S C = A H A C = A M A I
⇒ MJ = x a . 3 a = x 3
MH = x a . 3 a = x 3
JH = x a . 2 a = 2x
Chu vi thiết diện MHJ là: x 3 + x 3 + 2x = 2x ( 3 + 1 )
Đáp án A
Qua M kẻ đường thẳng song song với IC cắt AC tại E và kẻ đường thẳng song song với SI cắt SA tại D.
Khi đó thiết diện của mặt phẳng với tứ diện là tam giác MED
Lại có: MD // SI ⇒ A M A I = M D S I
ME // IC ⇒ A M A I = M E I C
Do đó M D S I = M E I C
Vì S.ABC là tứ diện đều nên SI = CI (hai đường trung tuyến trong hai tam giác đều có chung cạnh)
Suy ra MD = ME
Vậy tam giác MED cân tại M.
Đáp án B