Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


27.
Bán kính mặt cầu ngoại tiếp tứ diện vuông được tính bằng:
\(R=\sqrt{\dfrac{OA^2+OB^2+OC^2}{4}}=\sqrt{\dfrac{1^2+2^2+3^2}{4}}=\dfrac{\sqrt{14}}{2}\)
28.
Từ giả thiết suy ra \(A\left(2;2;2\right)\)
Gọi điểm thuộc mặt Oxz có tọa độ dạng \(D\left(x;0;z\right)\)
\(\Rightarrow\overrightarrow{AD}=\left(x-2;-2;z-2\right)\)
\(\overrightarrow{BD}=\left(x+2;-2;z\right)\) ; \(\overrightarrow{CD}=\left(x-4;-1;z+1\right)\)
D cách đều A, B, C \(\Rightarrow\left\{{}\begin{matrix}AD=BD\\AD=CD\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left(x-2\right)^2+4+\left(z-2\right)^2=\left(x+2\right)^2+4+z^2\\\left(x-2\right)^2+4+\left(z-2\right)^2=\left(x-4\right)^2+1+\left(z+1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+z=1\\2x-3z=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}z=-\dfrac{1}{2}\\x=\dfrac{3}{4}\end{matrix}\right.\)
\(\Rightarrow P\left(\dfrac{3}{4};0;-\dfrac{1}{2}\right)\)
29.
Do tâm I mặt cầu thuộc Oz nên tọa độ có dạng: \(I\left(0;0;z\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AI}=\left(-3;1;z-2\right)\\\overrightarrow{BI}=\left(-1;-1;z+2\right)\end{matrix}\right.\)
Mặt cầu qua A, B nên \(AI=BI\)
\(\Leftrightarrow3^2+1^2+\left(z-2\right)^2=1^2+1^2+\left(z+2\right)^2\)
\(\Leftrightarrow8z=8\Rightarrow z=1\)
\(\Rightarrow I\left(0;0;1\right)\Rightarrow R=IB=\sqrt{1^2+1^1+3^2}=\sqrt{11}\)
Phương trình mặt cầu:
\(x^2+y^2+\left(z-1\right)^2=11\)

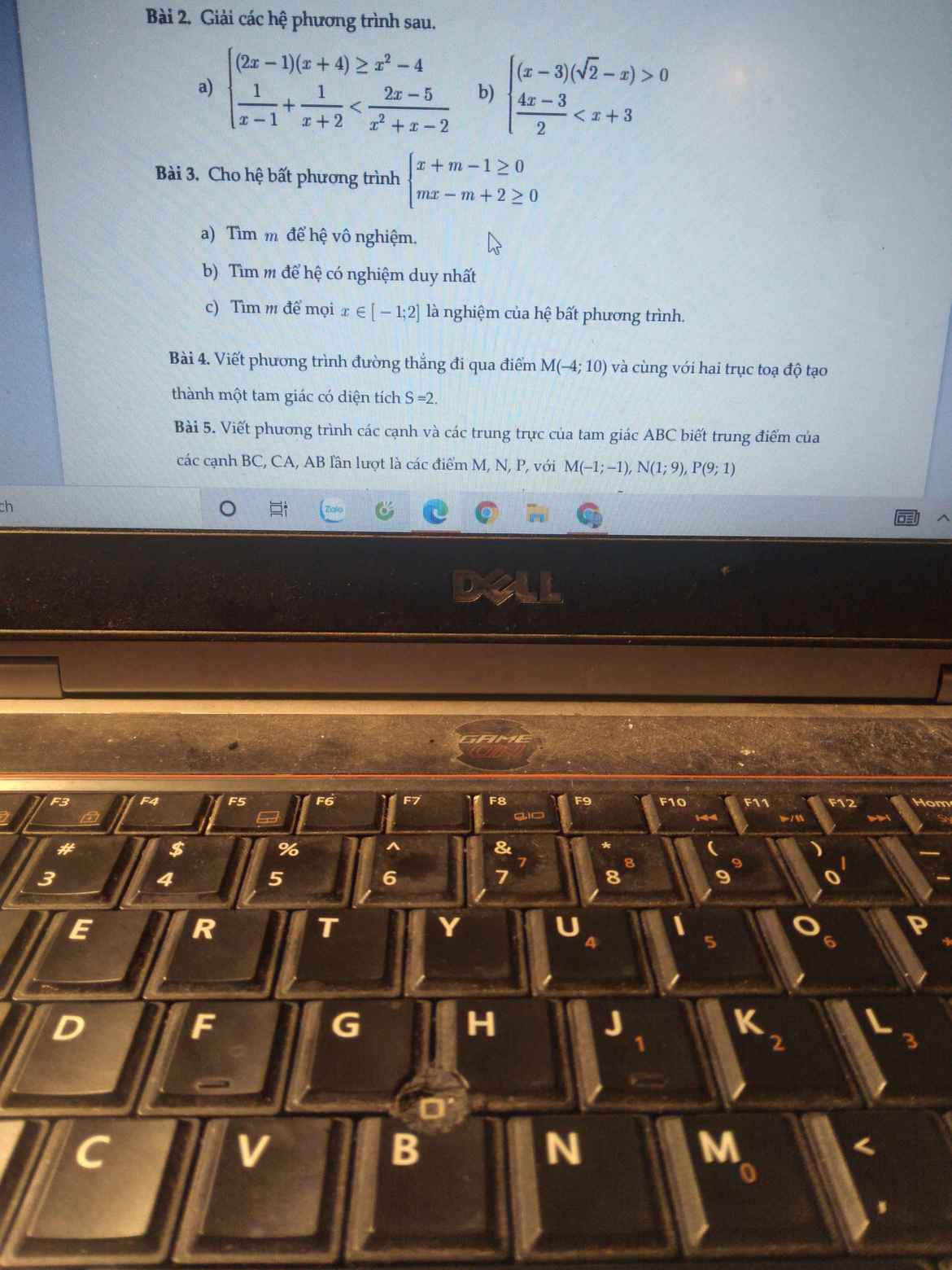
C3: Hệ bpt trở thành: \(\left\{{}\begin{matrix}x\ge1-m\\mx\ge2-m\end{matrix}\right.\)
a, Để hệ phương trình vô nghiệm thì \(m=0\)
b, Để hệ có nghiệm duy nhất thì \(\left\{{}\begin{matrix}m\ne0\\\dfrac{m-2}{m}=1-m\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}m\ne0\\m=\pm\sqrt{2}\end{matrix}\right.\) \(\Leftrightarrow\) \(m=\pm\sqrt{2}\)
c, \(x\in\left[-1;2\right]\) \(\Leftrightarrow\) \(-1\le x\le2\)
Để mọi \(x\in\left[-1;2\right]\) là nghiệm của hệ bpt trên thì
\(\left\{{}\begin{matrix}-1\le1-m\le2\\-1\le\dfrac{2-m}{m}\le2\end{matrix}\right.\) với \(m\ne0\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}2\ge m\ge-1\\m\ge\dfrac{2}{3}\end{matrix}\right.\) \(\left(m\ne0\right)\)
\(\Leftrightarrow\) \(2\ge m\ge\dfrac{2}{3}\)
Vậy \(m\in\left[\dfrac{2}{3};2\right]\) thì mọi \(x\in\left[-1;2\right]\) là nghiệm của hệ bpt
Chúc bn học tốt!




PTHH : 2Al + 6HCl --> 2AlCl3 + 3H2 ↑ (1)
nAlCl3 = \(\dfrac{m}{M}=\dfrac{13,35}{27+35,5.3}=0.1\left(mol\right)\)
Từ (1) => nHCl = 2nH2 = 0.2 (mol)
=> mHCl = n.M = 0.2 x 36.5 = 7.3 (g)
\(PTHH:2Al+6HCl\rightarrow2AlCl_3+3H_2\\ n_{AlCl_3}=\dfrac{m}{M}=\dfrac{13,35}{133,5}=0,1\left(mol\right)\\ Theo.PTHH:n_{HCl}=3.n_{AlCl_3}=3.0,1=0,3\left(mol\right)\\ m_{HCl}=n.M=0,3.36,5=10,95\left(g\right)\)


\(\Leftrightarrow sinx+sinax=\sqrt{3}cosx-\sqrt{3}cosax\)
\(\Leftrightarrow sinax+\sqrt{3}cosax=\sqrt{3}cosx-sinx\)
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}cosax+\dfrac{1}{2}sinax=\dfrac{\sqrt{3}}{2}cosx-\dfrac{1}{2}sinx\)
\(\Leftrightarrow cos\left(ax-\dfrac{\pi}{6}\right)=cos\left(x+\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}ax-\dfrac{\pi}{6}=x+\dfrac{\pi}{6}+k2\pi\\ax-\dfrac{\pi}{6}=-x-\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(a-1\right)x=\dfrac{\pi}{3}+k2\pi\\\left(a+1\right)x=k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3\left(a-1\right)}+\dfrac{k2\pi}{a-1}\left(a\ne1\right)\\x=\dfrac{k2\pi}{a+1}\left(a\ne-1\right)\end{matrix}\right.\)

Phương trình hoành độ giao điểm (d) và (P):
\(x^2-2x-3=ax-a-3\)
\(\Leftrightarrow x^2-\left(a+2\right)x+a=0\)
\(\Delta=\left(a+2\right)^2-4a=a^2+4>0;\forall a\Rightarrow\) (d) luôn cắt (P) tại 2 điểm pb
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_A+x_B=a+2\\x_Ax_B=a\end{matrix}\right.\)
Mặt khác do A, B thuộc (d) nên: \(\left\{{}\begin{matrix}y_A=ax_A-a-3\\y_B=ax_B-a-3\end{matrix}\right.\)
\(y_A+y_B=0\)
\(\Leftrightarrow a\left(x_A+x_B\right)-2a-6=0\)
\(\Leftrightarrow a\left(a+2\right)-2a-6=0\)
\(\Leftrightarrow a^2-6=0\)
\(\Leftrightarrow a=\pm\sqrt{6}\)






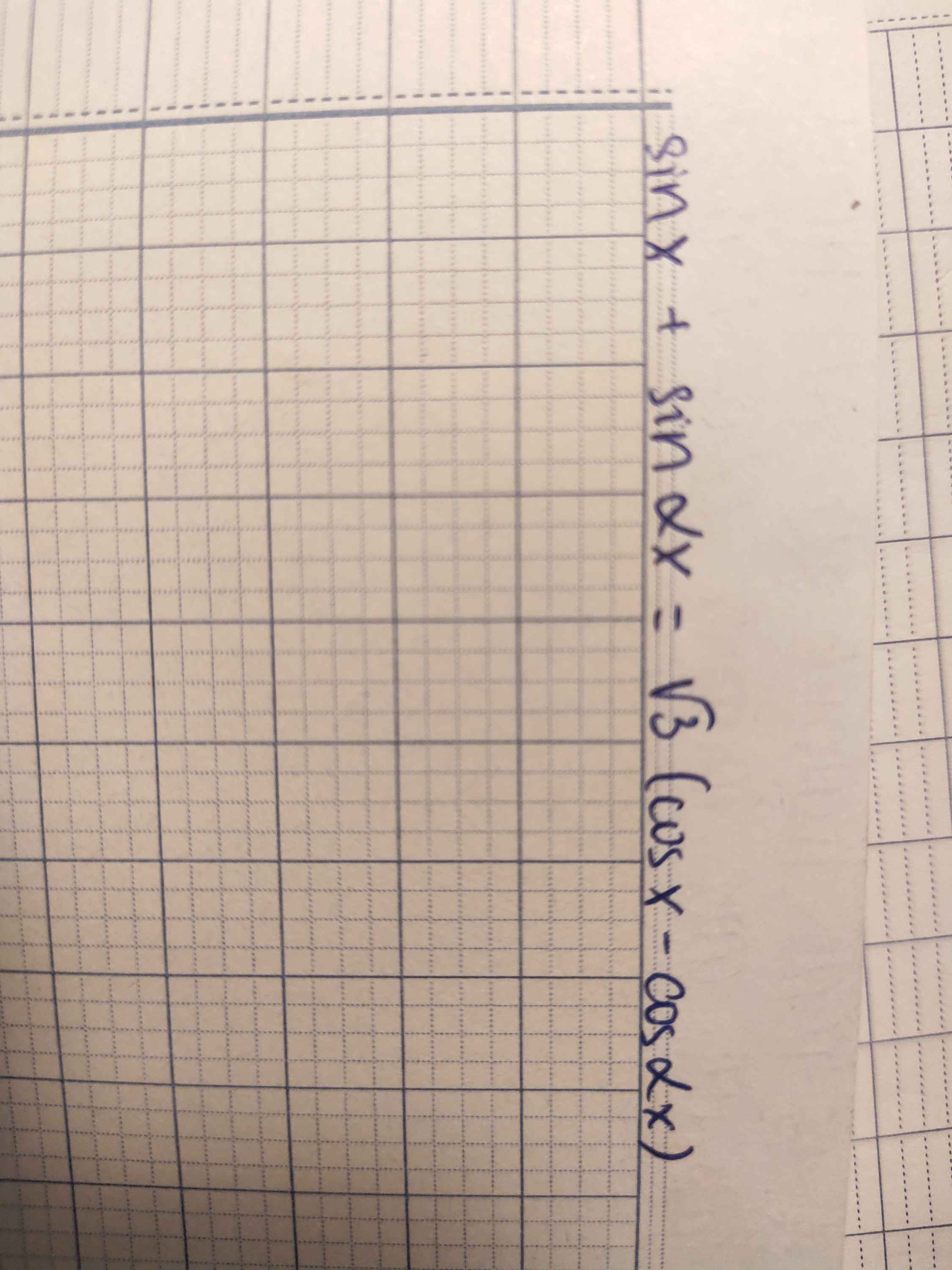

bài đâu bn