Cho hàm số f(x) có đạo hàm f ' ( x ) = x + 1 2 ( x - 3 ) . Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực đại tại x = 3
B. Hàm số đạt cực tiểu tại x = 3
C. Hàm số đạt cực tiểu tại x = -1
D. Hàm số đạt cực đại tại x = -1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Ta có: f ' x > 0 ⇔ - 3 < x < 2 f ' x < 0 ⇔ [ x > 2 x < - 3
Suy ra hàm số đồng biến trên khoảng (-3;2), nghịch biến trên các khoảng - ∞ ; - 3 v à 2 ; + ∞ .

Chọn D
Xét hàm số ![]() . Khi đó hàm số
. Khi đó hàm số ![]() liên tục trên các đoạn
liên tục trên các đoạn ![]() ,
, ![]() và có
và có ![]() là một nguyên hàm của hàm số
là một nguyên hàm của hàm số ![]() .
.
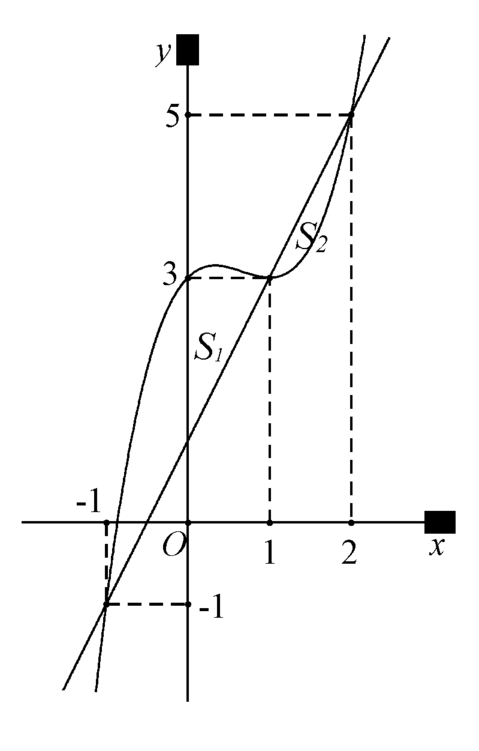
Do đó diện tích hình phẳng giới hạn bởi  là
là
![]()
![]()
![]()
![]() .
.
Vì ![]() nên
nên ![]() .
.
Diện tích hình phẳng giới hạn bởi 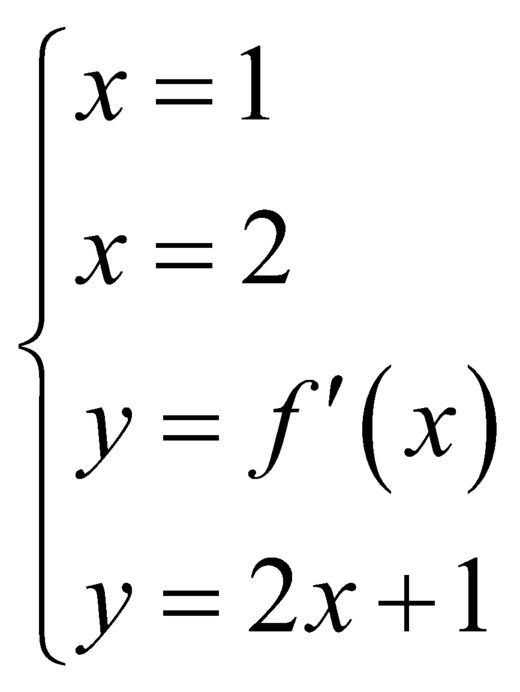 là
là
![]()
![]()
![]()
![]() .
.
Vì ![]() nên
nên ![]() .
.

Đáp án C
Từ giả thiết em có f ' x = − x − 1 2 − 1 < 0 , ∀ x ∈ ℝ . Hàm số f(x) luôn nghịch biến trên − ∞ ; + ∞ .

Chọn D
Xét hàm số g(x) = f(x) - 1 3 x 3 - 3 4 x 2 + 3 2 x + 2018 .
![]()
Cho ![]()
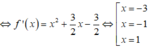
Dựa vào đồ thị ta so sánh được m i n [ - 3 ; 1 ] g ( x ) = g(-1)

Chọn D
Cho hàm số y = f(x). Đồ thị hàm số đạo hàm y = f'(x) như hình vẽ dưới đây. Xét hàm số
![]()
![]()
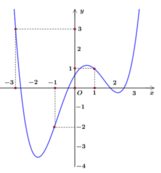
Cho ![]()
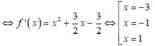
Dựa vào đồ thị ta so sánh được ![]()
Đáp án B
Phương pháp:
Nếu f'(x) đổi dấu khi qua điểm x = x0 ⇒ x = x0 là điểm cực trị của hàm số.
Cách giải:
f'(x) đổi dấu từ - sang + tại x = 3 ⇒ Hàm số đạt cực tiểu tại x = 3