Số giá trị nguyên của tham số m để phương trình m - x 3 + 2 x - 3 = 4 có ba nghiệm phân biệt là
A. 7
B. 6
C. 5
D. 8
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 3 2023
\(f^2\left(\left|x\right|\right)-\left(m-6\right)f\left(\left|x\right|\right)-m+5=0\) có \(a-b+c=0\) nên có các nghiệm \(\left[{}\begin{matrix}f\left(\left|x\right|\right)=-1\\f\left(\left|x\right|\right)=m-5\end{matrix}\right.\)
- Với \(f\left(\left|x\right|\right)=-1\Rightarrow\left|x\right|^2-4\left|x\right|+3=-1\Rightarrow\left|x\right|=2\Rightarrow x=\pm2\) có 2 nghiệm
- Xét \(f\left(\left|x\right|\right)=m-5\Leftrightarrow\left|x\right|^2-4\left|x\right|+8=m\) (1)
Từ BBT của \(y=\left|x\right|^2-4\left|x\right|+8\) dễ dàng suy ra (1) có 4 nghiệm pb khi \(4< m< 8\)
\(\Rightarrow m=\left\{5;6;7\right\}\) có 3 giá trị nguyên
14 tháng 8 2021
\(\Delta'=b'^2-ac=\left(m-1\right)^2-\left(m^2-3\right)=4-2m\)
Để pt có 2 nghiệm pb : \(m< 2\)
Theo định lí vi - et :
\(\left\{{}\begin{matrix}x_1+x_2=m-1\\x_1.x_2=m^2-3\end{matrix}\right.\)
Mà \(x_1=3x_2\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x_2=m-1\\3x^2_2=m^2-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{m-1}{4}\\x_2=\pm\dfrac{\sqrt{m^2-3}}{\sqrt{3}}\end{matrix}\right.\)
CM
29 tháng 9 2019
Đáp án C
Điều kiện x ≥ 3 2
Ta có PT:
m − x 3 + 2 x − 3 = 2 ⇔ m − x 3 = 2 − 2 x − 3
⇔ m − x = 2 − 2 x − 3 3 ⇔ m = x + 2 − 2 x − 3 3
Xét hàm số: f x = x + 2 − 2 x − 3 3
⇒ f ' x = 1 + 3 2 − 2 x − 3 2 . − 1 2 x − 3 = 2 x − 3 − 3 2 − 2 x − 3 2 2 x − 3 = 2 x − 3 − 2 − 3 2 − 2 x − 3 2 + 2 2 x − 3
Đặt 2 x − 3 − 2 = t t ≥ − 2
⇒ f ' t = − 3 t 2 + t + 2 t − 2 ⇒ f ' t = 0 ⇔ t = 1 ⇒ x = 6 t = − 2 3 ⇒ x = 43 18
Ta có BBT của f(x) như sau:
Dựa vào BBT ta thấy để PT đã cho có 3 nghiệm phân biệt thì 2 , 4 < m < 5 với m nguyên ⇒ m ∈ 3 ; 4
AH
Akai Haruma
Giáo viên
16 tháng 5 2021
Lời giải:
Đặt $\sqrt{x+2}=t(t\geq 0)$ thì pt trở thành:
$t^2-2-2t-m-3=0$
$\Leftrightarrow t^2-2t-(m+5)=0(*)$
Để PT ban đầu có 2 nghiệm pb thì PT $(*)$ có 2 nghiệm không âm phân biệt.
Điều này xảy ra khi \(\left\{\begin{matrix} \Delta'=1+m+5>0\\ S=2>0\\ P=-(m+5)\geq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m>-6\\ m\leq -5\end{matrix}\right.\)
Đáp án B.
Đáp án B
Phương pháp:
+) Thế vào phương trình, lập phương hai vế, cô lập m, đưa phương trình về dạng m = f(t)
+) Khảo sát và lập BBT của hàm số y = f(t), t ≥ 0 Biện luận để phương trình có 2 nghiệm phân biệt.
Cách giải:
Ta có:
Bảng biến thiên:
Để phương trình có 3 nghiệm phân biệt t ≥ 0 thì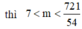
⇒ m ∈ 8 ; 9 ; 10 ; 11 ; 12 ; 13
⇒ Có 6 giá trị nguyên của m thỏa mãn.