Tìm giá trị thực của tham số m để phương trình (m2-5m+6)x=m2-2m vô nghiệm
giúp mình với đang cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 2 bạn ghi thiếu đề
Câu 1:
\(\Leftrightarrow\left(m^2-3m\right)x+2x< 2-m\)
\(\Leftrightarrow\left(m^2-3m+2\right)x< 2-m\)
BPT đã cho vô nghiệm khi và chỉ khi:
\(\left\{{}\begin{matrix}m^2-3m+2=0\\2-m\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m=1\\m=2\end{matrix}\right.\\m\ge2\end{matrix}\right.\) \(\Rightarrow m=2\)

Đáp án C
Đặt t = x ≥ 0 , khi đó PT đã cho trở thành 2 t 2 + t + m 2 − 2 m = 0 ⇔ 2 t 2 + t = − m 2 + 2 m
Hàm số y = 2 t 2 + t đồng biến trên 0 ; + ∞ .
Để PT đã cho có nghiệm thì − m 2 + 2 m ≥ y 0 ⇔ − m 2 + 2 m ≥ 1 ⇔ m − 1 2 ≤ 0 ⇔ m = 1

Thay x=2 vào pt ta có:
\(\left(m^2+2m+3\right)x-6=0\\ \Leftrightarrow2\left(m^2+2m+3\right)-6=0\\ \Leftrightarrow2m^2+4m+6-6=0\\ \Leftrightarrow2m+4m=0\\ \Leftrightarrow2m\left(m+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=0\\m=-2\end{matrix}\right.\)
Vậy ...

Điều kiện:
cos x # 0 ⇔ x # π 2 + k π , k ∈ ℝ .
Ta có:
![]()
![]()
Đặt t=log|cosx|. Do 0 < | cos x | ≤ 1 nên log cos x ≤ 0 hay t ∈ ( - ∞ ; 0 ]
Phương trình trở thành t 2 - 2 m t - m 2 + 4 = 0 *
có ∆ ' = m 2 + m 2 - 4 = 2 m 2 - 4
Phương trình đã cho vô nghiệm nếu và chỉ nếu phương trình (*) vô nghiệm hoặc có 2 nghiệm (không nhất thiết phân biệt) t 1 , t 2 thỏa mãn 0 < t 1 ≤ t 2
TH1: (*) vô nghiệm ![]()
TH2: (*) có hai nghiệm thỏa mãn 0 < t 1 ≤ t 2
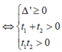
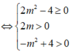
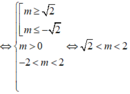
Kết hợp hai trường hợp ta được m ∈ - 2 ; 2
Chọn đáp án C.

(m - 2)x2 + 2(2m - 3)x + 5m - 6 = 0 (1)
- Nếu m - 2 = 0 ⇔ m = 2, khi đó phương trình (1) trở thành:
2x + 4 = 0 ⇔ x = -2 hay phương trình (1) có một nghiệm
Do đó m = 2 không phải là giá trị cần tìm.
- Nếu m - 2 ≠ 0 ⇔ m ≠ 2 ta có:
Δ' = (2m - 3)2 - (m - 2)(5m - 6)
= 4m2 - 12m + 9 - 5m2 + 6m + 10m - 12
= -m2 + 4m - 3 = (-m + 3)(m - 1)
(1) vô nghiệm ⇔ Δ' < 0 ⇔ (-m + 3)(m - 1) < 0 ⇔ m ∈ (-∞; 1) ∪ (3; +∞)
Vậy với m ∈ (-∞; 1) ∪ (3; +∞) thì phương trình vô nghiệm.

Chọn C.
Phương pháp:
- Đặt t = log cos x và tìm điều kiện của t .
- Thay vào phương trình đã cho đưa về phương trình ẩn t .
- Biến đổi điều kiện bài toán về điều kiện của phương trình vừa có được và tìm m .
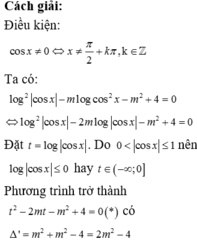

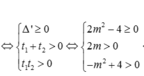
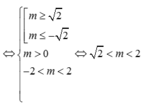
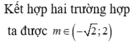
\(\Leftrightarrow\left(m^2-5m+6\right)x-m^2+2m=0\)
PT vô nghiệm \(\Leftrightarrow\left\{{}\begin{matrix}m^2-5m+6=0\\-m^2+2m\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m=3\\m=2\end{matrix}\right.\\\left\{{}\begin{matrix}m\ne0\\m\ne2\end{matrix}\right.\end{matrix}\right.\Leftrightarrow m=3\)
Giúp em câu e bài 1 với ạ