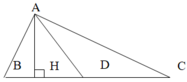
Trong hình bên AH là đường cao của mấy hình tam giác
A. 2
B. 4
C. 6
D. 8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔABC, ΔAHB,ΔAHM, ΔAMC
b: 1 góc tù: ΔAMC
1 góc vuôg: ΔAHB; ΔAHC

a.
AH là đường cao của các tam giác ABC, AMB và AMC
b.
Độ dài cạnh MC là:
\(2\times24:8=6\left(cm\right)\)
Độ dài đáy BC là:
\(6\times2=12\left(cm\right)\)
c.
Diện tích tam giác ABC là:
\(8\times12:2=48\left(cm^2\right)\)

Phương pháp giải:
- Đếm các hình tam giác đơn.
- Ghép hình, đếm tiếp cho đến hết tất cả các hình tam giác.
Lời giải chi tiết:
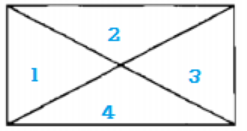
Hình trên có các hình tam giác là: 1; 2; 3; 4; 1+2; 2+3; 3+4; 4 +1.
Chọn đáp án D. 8.

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Vậy: BC=10cm
a) Xét ΔABC có
BD là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)(Tính chất tia phân giác của tam giác)
hay \(\dfrac{AD}{6}=\dfrac{CD}{10}\)
mà AD+CD=AC=8(cm)(D nằm giữa A và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau,ta được:
\(\dfrac{AD}{6}=\dfrac{CD}{10}=\dfrac{AD+CD}{6+10}=\dfrac{8}{16}=\dfrac{1}{2}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{AD}{6}=\dfrac{1}{2}\\\dfrac{CD}{10}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AD=3\left(cm\right)\\CD=5\left(cm\right)\end{matrix}\right.\)
Vậy: AD=3cm; CD=5cm
Đáp án là C