Cho hình vẽ sau, hãy chọn câu sai trong các câu sau
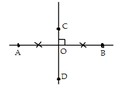
A. CD là đường trung trực của đoạn thẳng AB
B. AB là đường trung trực của đoạn thẳng CD
C. A O C ⏜ = B O D ⏜
D. AO = OB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : – Góc x’Oy’ và góc xOy là hai góc đối đỉnh ⇒ góc xOy = góc x’Oy’ = 90o
– ∠(xOy) và ∠(xOy’) là hai góc kề bù ⇒ ∠(xOy) + ∠(xOy’) = 180o
⇒ (xOy’) = 180o – (xOy) = 180o– 90o = 90o
– ∠(xOy’) và ∠(x’Oy) là hai góc đối đỉnh ⇒ ∠(xOy’) = ∠(x’Oy) = 90o
Khi đó các góc ∠yOx’ ; ∠x’Oy’ ; ∠y’Ox cũng đều là những góc vuông
Trả lời câu hỏi Toán 7 Tập 1 Bài 2 trang 84: Vẽ phác hai đường thẳng a và a’ vuông góc với nhau và viết kí hiệu.Lời giải
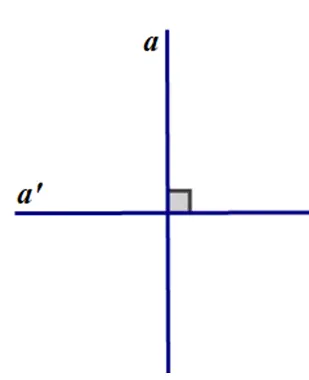


I là trung điểm của AB nên IA = IB = 1 2 AB = 1 2 .12 = 6 cm
M thuộc đường trung trực của đoạn thẳng AB nên MB = MA = 10 cm
MI là đường trung trực của AB nên MI ⊥ AB
Suy ra tam giác AMI vuông tại I
Áp dụng định lý Py – ta – go ta có: M A 2 = M I 2 + A I 2
⇒ M I 2 = M A 2 − A I 2 = 10 2 − 6 2 = 64
⇒ M I = 64 = 8 cm
Ta có: MA = MB; AI = BI ; MI cạnh chung
Do đó: Δ A M I = Δ B M I (c – c – c)
Suy ra M A I ^ = M B I ^
Vậy A, B, C đúng và D sai (do MA = MB ≠ MI).
Chọn đáp án D
B là sai vì M và I là 2 điểm trùng nhau
D là sai vì MB=8CM; MA=10CM; MB=10CM nên ko thể là MB=MA=MI mà phải là MA=MB>MI

+) Do tam giác ABD cân tại D nên DA = DB ( định nghĩa tam giác cân).
Suy ra: D nằm trên đường trung trực của AB. (1)
+) Do tam giác ABC là tam giác đều nên CA = CB
Suy ra: C nằm trên đường trung trực của AB (2)
Từ (1) và (2)suy ra: CD là đường trung trực của AB.
+) Do E là trung điểm của AB nên EA = EB
Suy ra E nằm trên đường trung trực của AB
Suy ra, E nằm trên đường thẳng CD.
Do đó, (B) sai .
Chọn B.

Ta có: b b ' ⊥ a a ' nên b b ' ⊥ A B tại (vì hai điểm và thuộc đường thẳng aa' ) (1)
và M là trung điểm của AB (2)
Từ (1) và (2) suy ra nên bb' là đường trung trực của AB (theo định nghĩa đường trung trực)
Tương tự: aa' là đường trung trực của CD.
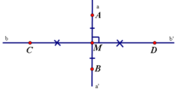

Xét \(\Delta\)ABC và \(\Delta\) ABD ta có: AB chung;
góc ABC = góc ABD
góc CAB = góc DAB
⇒ \(\Delta\) ABC = \(\Delta\) ABD (g-c-g)
⇒ BC = BD
AC = AD
BC = BD ⇒ \(\Delta\) CBD cân tại B mà AB là phân giác của góc CBD nên
⇒ AB là trung trực của CD vì trong tam giác cân đường cao cũng là đường trung trực, đường phân giác.
b, Xét \(\Delta\) ACD có
AM = AC;
AN = ND
⇒ MN là đường trung bình của tam giác ACD
⇒ MN//CD (đpcm)
c, AC = AD (cmt)
⇒ AN = AM = \(\dfrac{1}{2}AC\)
Xét tam giác AMB và tam giác ANB ta có:
AB chung; AN = AM
góc NAB = góc BAM
⇒ \(\Delta\) AMB = \(\Delta\) ANB (c-g-c)
⇒ Góc AMB = góc ANB (đpcm)

- Vẽ đoạn thẳng AB = 24mm
- Vẽ trung điểm I cuả AB
Vì I là trung điểm của AB nên IA = IB = AB/2 = 12 (mm)
Đặt thước thẳng trùng với đường thẳng AB sao cho vạch 0 trùng với điểm A , vạch 12 cho ta vị trí điểm I.
- Vẽ đường thẳng d đi qua I và d⊥ AB
Đặt êke sao cho một cạnh góc vuông của êke trùng với đường thẳng AB, đỉnh góc vuông của êke trùng với I, vẽ đường thẳng đi qua cạnh góc vuông còn lại của êke ta được đường thẳng d.
Khi đó d là trung trực của AB.
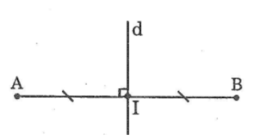
Quan sát hình vẽ đã cho ta thấy
+ AO = OB (D đúng) ⇒ O là trung điểm của AB (1)
+ CD ⊥ AB tại O (2) ⇒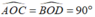 ⇒ C đúng
⇒ C đúng
Từ (1) và (2) suy ra CD là đường trung trực của đoạn thẳng AB ⇒ A đúng
+ Vì OC ≠ OD suy ra AB không phải là đường trung trực của CD ⇒ B sai
Chọn đáp án B