Tìm 4 số chẵn thiết lập bỡi ba chữ số sau 1,2,3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 2 2019
Gọi tập hợp E = {0,1,2,3,4,5}
c) Số tự nhiên có 3 chữ số có dạng
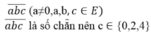
Có ba cách chọn chữ số c ( vì c ∈ {0,2,4}).
Ứng với mỗi cách chọn c , có 6 cách chọn chữ số b (vì b ∈ E)
ứng với mỗi cách chọn c, b có 5 cách chọn chữ số a (vì a ∈ E và a≠ 0)
Áp dụng quy tắc nhân ta có 3*6*5 = 90 số có 3 chữ số.
Vì vậy đáp án là B
6L
3
27 tháng 9 2023
a) Việc lập số chẵn gồm ba chữ số là thực hiện 3 hành động liên tiếp: chọn chữ số hàng đơn vị, chọn chữ số hàng chục, chọn chữ số hàng trăm.
chọn chữ số hàng đơn vị: Có 3 cách chọn (số 2, 4, 6).
chọn chữ số hàng chục: Có 7 cách chọn.
chọn chữ số hàng trăm: Có 7 cách chọn.
Theo quy tắc nhân, số số chẵn lập được là: 3.7.7=147 (số).
b) Việc lập số chẵn gồm ba chữ số đôi một khác nhau là thực hiện 3 hành động liên tiếp: chọn chữ số hàng đơn vị, chọn chữ số hàng chục, chọn chữ số hàng trăm.
chọn chữ số hàng đơn vị: Có 3 cách chọn (số 2, 4, 6).
chọn chữ số hàng chục: Có 6 cách chọn.
chọn chữ số hàng trăm: Có 5 cách chọn.
Theo quy tắc nhân, số số chẵn lập được là: 3.6.5=90 (số).
CM
31 tháng 7 2018
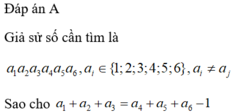
Vậy số cách để lập số có 6 chữ số khác nhau sao cho tổng ba số đầu nhỏ hơn tổng ba số cuối một đơn vị là: 
