chứng minh rằng các cặp số sau ;à số nguyên tố cùng nhau:
a) 6n+10 và 2n+3
b)2n+1 và 6n+5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: (-a) . b = - (a . b) = a . (-b).
Do đó 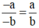 (theo định nghĩa SGK).
(theo định nghĩa SGK).

Ta có: (-a) . b = - (a . b) = a . (-b).
Do đó 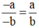 (theo định nghĩa SGK).
(theo định nghĩa SGK).

Gọi d là ước chung lớn nhất của 2 số. Nhiệm vụ của ta là chứng minh d=1.
a) 2n+3, n+2 \(⋮d\)
\(\Rightarrow\left(2n+3\right)-\left(n+2\right)⋮d\)
\(\Rightarrow1⋮d\)
b) n+1, 3n+4
\(\Rightarrow\left(3n+4\right)-3\left(n+1\right)⋮d\)
\(\Rightarrow1⋮d\)
c) 2n+3, 3n+4
\(\Rightarrow3\left(2n+3\right)-2\left(3n+4\right)⋮d\)
\(\Rightarrow1⋮d\)
𝓪, 𝓖𝓸̣𝓲 𝓤̛𝓒𝓛𝓝\(\left(2n+3,n+2\right)=d\)
\(\Rightarrow2n+3⋮d\)
\(\Rightarrow n+2⋮d\Rightarrow2.\left(n+2\right)⋮d\Rightarrow2n+4⋮d\)
\(\Rightarrow2n+4-2n+3⋮d\Rightarrow1⋮d\Rightarrow d=1\)
\(\Rightarrow\)𝓤̛𝓒𝓛𝓝\(\left(2n+3,n +2\right)=1\)
𝓥𝓪̣̂𝔂 \(2n+3,n+2\) 𝓵𝓪̀ 𝓱𝓪𝓲 𝓼𝓸̂́ 𝓷𝓰𝓾𝔂𝓮̂𝓷 𝓽𝓸̂́ 𝓬𝓾̀𝓷𝓰 𝓷𝓱𝓪𝓾

gọi UCLN﴾2n + 1 ; 6n + 5﴿ là d
ta có :
2n + 1 chia hết cho d =>3(2n+1) chia hết cho d=>6n+3 chia hết cho d
6n + 5 chia hết cho d
=> [﴾6n + 5﴿ ‐ ﴾6n + 3﴿] chia hết cho d
=>2 chia hết cho d
=> d thuộc Ư﴾2﴿ = {1;2}
Mà 2n + 1 ; 6n + 5 lẻ nên n = 1
=>UCLN(..)=1
=>ntcn

a) Ta cần chứng minh \(\frac{ab}{abab}=\frac{3}{303}\) . Ta có :
\(\frac{ab}{abab}=\frac{ab\div ab}{abab\div ab}=\frac{1}{101}\left(1\right)\) và \(\frac{3}{303}=\frac{3\div3}{303\div3}=\frac{1}{101}\left(2\right)\)
Từ \(\left(1\right)\left(2\right)\Rightarrow\frac{ab}{abab}=\frac{3}{303}\Leftrightarrowđpcm\)
b) Ta cần chứng minh\(\frac{7x-21}{14x-42}=\frac{2}{4}\) . Ta có :
\(\frac{7x-21}{14x-42}\Leftrightarrow2.\frac{7x-21}{14x-42}=\frac{2\left(7x-21\right)}{14x-42}=\frac{14x-42}{14x-42}=1\left(1\right)\)
\(\frac{2}{4}=\frac{1}{2}\Leftrightarrow2.\frac{1}{2}=\frac{2.1}{2}=\frac{2}{2}=1\left(2\right)\) . Từ \(\left(1\right)\left(2\right)\)
\(\frac{14x-42}{14x-42}=\frac{2}{2}=1\Rightarrow\frac{7x-21}{14x-42}=\frac{2}{4}\Leftrightarrowđpcm\)

làm mẫu một bài nha :))
gợi UCLN(3n+4,n+1) =d. ta có:
\(\hept{\begin{cases}3n+4⋮d\\n+1⋮d\end{cases}\Rightarrow\hept{\begin{cases}3n+4⋮d\\3n+3⋮d\end{cases}}}\Rightarrow\left[\left(3n+4\right)-\left(3n+3\right)\right]⋮d\)
\(\Rightarrow1⋮d\Rightarrow d=1\)
vì (3n+4,n+1) =1 => \(\frac{3n+4}{n+1}\)là phân số tối giản
chữa đề : chứng minh rằng các cặp số sau là số nguyên tố cùng nhau