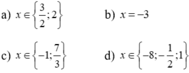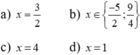Giải các phương trình sau: (2x - 1)(x – 3)(3x + 7) = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)
\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)
\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)
\(\Leftrightarrow x^2-9-x^2+3x=0\)
\(\Leftrightarrow3x-9=0\)
\(\Leftrightarrow3x=9\)
\(\Leftrightarrow x=3\left(n\right)\)
Vậy \(S=\left\{3\right\}\)
\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)
\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)
\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)
\(\Leftrightarrow12x-9-12x+20+2x-7>0\)
\(\Leftrightarrow2x+4>0\)
\(\Leftrightarrow2x>-4\)
\(\Leftrightarrow x>-2\)

1) \(\sqrt[]{3x+7}-5< 0\)
\(\Leftrightarrow\sqrt[]{3x+7}< 5\)
\(\Leftrightarrow3x+7\ge0\cap3x+7< 25\)
\(\Leftrightarrow x\ge-\dfrac{7}{3}\cap x< 6\)
\(\Leftrightarrow-\dfrac{7}{3}\le x< 6\)

a: =>(x-3)(x+1)=0
=>x=3 hoặc x=-1
b: =>x(x-3)=0
=>x=0 hoặc x=3
c: =>(x-5)(x+1)=0
=>x=5 hoặc x=-1
d: =>5x^2+7x-5x-7=0
=>(5x+7)(x-1)=0
=>x=1 hoặc x=-7/5
e: =>x^2-4=0
=>x=2 hoặc x=-4
h: =>x^2-4x+4-3=0
=>(x-2)^2=3
=>\(x=2\pm\sqrt{3}\)

Bạn cần viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) đẻ được hỗ trợ tốt hơn. Viết như thế kia rất khó đọc => khả năng bị bỏ qua bài cao.
a: =>3x=3
=>x=1
b: =>12x-2(5x-1)=3(8-3x)
=>12x-10x+2=24-9x
=>2x+2=24-9x
=>11x=22
=>x=2
c: =>2x-3(2x+1)=x-6x
=>-5x=2x-6x-3=-4x-3
=>-x=-3
=>x=3
d: =>2x-5=0 hoặc x+3=0
=>x=5/2 hoặc x=-3
e: =>x+2=0
=>x=-2

`3x+7=0`
`<=>3x=-7`
`<=>x=-7/3`
Vậy `S={-7/3}`
______________________
`2x(x-2)+2x(5-3x)=0`
`<=>2x(x-2+5-3x)=0`
`<=>2x(3-2x)=0`
`@TH1:2x=0<=>x=0`
`@TH2: 3-2x=0<=>2x=3<=>x=3/2`
Vậy `S={0;3/2}`
3x+7=0
\(\Leftrightarrow3x=-7\Leftrightarrow x=-\dfrac{7}{3}\)
2x(x-2)+2x(5-3x)=0
\(\Leftrightarrow2x\left(x-2+5-3x\right)=0\)
\(\Leftrightarrow2x\left(-2x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=0\\-2x=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{-3}{-2}=\dfrac{3}{2}\end{matrix}\right.\)

a: 5-3x=6x+7
=>-3x-6x=7-5
=>-9x=2
=>\(x=-\dfrac{2}{9}\)
b: \(\dfrac{3x-2}{6}-5=3-\dfrac{2\left(x+7\right)}{4}\)
=>\(\dfrac{3x-2}{6}+\dfrac{x+7}{2}=8\)
=>\(\dfrac{3x-2+3\left(x+7\right)}{6}=8\)
=>3x-2+3x+14=48
=>6x+12=48
=>6x=36
=>\(x=\dfrac{36}{6}=6\)
c: \(\left(x-1\right)\left(5x+3\right)=\left(3x-8\right)\left(x-1\right)\)
=>\(\left(x-1\right)\left(5x+3\right)-\left(3x-8\right)\left(x-1\right)=0\)
=>(x-1)(5x+3-3x+8)=0
=>(x-1)(2x+11)=0
=>\(\left[{}\begin{matrix}x-1=0\\2x+11=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{11}{2}\end{matrix}\right.\)
d: \(\left(2x-1\right)^2-\left(x+3\right)^2=0\)
=>\(\left(2x-1-x-3\right)\left(2x-1+x+3\right)=0\)
=>\(\left(x-4\right)\left(3x+2\right)=0\)
=>\(\left[{}\begin{matrix}x-4=0\\3x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-\dfrac{2}{3}\end{matrix}\right.\)