Tìm x biết: ( 2 x 2 ) ( x - 1 ) – ( x 2 ) . ( 2 x 1 ) = ...

PT

Pham Trong Bach

28 tháng 3 2018

Tìm x biết: ( 2 x + 2 ) ( x - 1 ) – ( x + 2 ) . ( 2 x + 1 ) = 0 A. - 4 5 B. - 1 5 C. ...

Đọc tiếp

#Toán lớp 8

1

CM

Cao Minh Tâm

28 tháng 3 2018

Đúng(0)

NT

Nguyễn Thị Minh Ánh

9 tháng 1 2017 - olm

tìm x,y thuộc Z ,biêt: (2x-1).(2x+1)=-35

tìm c,y thuộc Z , biết: (x+1)^2 + (y+1)^2 + (x-y)^2 =2

tìm x,y thuộc Z, biết: (x^2-8).(x^2-15)<0

tìm x,y thuộc Z biết: x=6.y và|x|-|y|=60

tìm a,b thuộc Z biết: |a|+|b|<2

#Toán lớp 6

0

HK

Hoàng Kiều Mẫn

4 tháng 11 2018 - olm

Bài 1 : Tìm x , biết :
a. |x-1|+|x-2|+....+|x-8| = 22
b. |x-1|+|x-2|+|x-3|+...+|x-100| = 2500
Bài 2 :
Tìm x , biết :
|x+1|+|x+2|+....+|x+100| = 605.x
Giúp tớ với ?

#Toán lớp 7

1

MN

Mất nick đau lòng con quốc quốc

4 tháng 11 2018

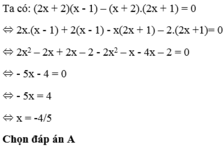
............................. Đấng Ed bảo ko chắc cho lắm nên sai thì sr nhé -,-

+) Với \(x\ge8\) ta có :

\(x-1+x-2+...+x-8=22\)

\(\Leftrightarrow\)\(8x-36=22\)

\(\Leftrightarrow\)\(x=\frac{29}{4}\)( không thỏa mãn )

+) Với \(x< 1\) ta có :

\(1-x+2-x+...+8-x=22\)

\(\Leftrightarrow\)\(36-8x=22\)

\(\Leftrightarrow\)\(x=\frac{7}{4}\) ( không thỏa mãn )

Vậy không có x thỏa mãn đề bài

+) Với \(x\ge100\) ta có :

\(x-1+x-2+x-3+...+x-100=2500\)

\(\Leftrightarrow\)\(100x-5050=2500\)

\(\Leftrightarrow\)\(x=\frac{151}{2}\) ( không thỏa mãn )

+) Với \(x< 1\) ta có :

\(1-x+2-x+3-x+...+100-x=2500\)

\(\Leftrightarrow\)\(5050-100x=2500\)

\(\Leftrightarrow\)\(x=\frac{51}{2}\) ( không thỏa mãn )

Vậy không có x thỏa mãn đề bài

Bài 2 :

+) Với \(x\ge-1\) ta có :

\(x+1+x+2+...+x+100=605x\)

\(\Leftrightarrow\)\(100x+5050=605x\)

\(\Leftrightarrow\)\(x=10\) ( thỏa mãn )

+) Với \(x< -100\) ta có :

\(-x-1-x-2-...-x-100=605x\)

\(\Leftrightarrow\)\(-100x-5050=605x\)

\(\Leftrightarrow\)\(x=\frac{-1010}{141}\) ( không thỏa mãn )

Vậy \(x=10\)

~ Đấng phắn ~

Đúng(0)

H

Hezlin

16 tháng 6 2023

cho bt: P=\(\dfrac{x^2+x}{x^2-2x+1}\):(\(\dfrac{x+1}{x}\)-\(\dfrac{1}{1-x}\)+\(\dfrac{2-x^2}{x^2-x}\))

a,tìm đkxđ rồi rút gọn

b,tính P biết |1+2x|=3

c,tìm x để P=\(\dfrac{-1}{2}\)

d,tìm x để P<1

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

16 tháng 6 2023

a: ĐKXĐ: x<>0; x<>1

\(P=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}:\dfrac{x^2-1+x+2-x^2}{x\left(x-1\right)}\)

\(=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}\cdot\dfrac{x\left(x-1\right)}{x+1}=\dfrac{x^2}{x-1}\)

b: |2x+1|=3

=>x=1(loại); x=-2(nhận)

Khi x=-2 thì P=4/-3=-4/3

c: P=-1/2

=>x^2/x-1=-1/2

=>2x^2=-x+1

=>2x^2+x-1=0

=>2x^2+2x-x-1=0

=>(x+1)(2x-1)=0

=>x=1/2; x=-1

Đúng(1)

NL

Ng Linhhh

25 tháng 12 2022

Tìm x biết.

1) 3(x-2) + 4(x-1) = 25 2) (5x-3)(x-2) = (x-1)(x-2) 3) (x-2)² = 4(x-1)²

#Toán lớp 8

3

TM

Trần Minh Hiếu

25 tháng 12 2022

\(3\left(x-2\right)+4\left(x-1\right)=25\)

\(\Leftrightarrow3x-6+4x-4=25\)

\(\Leftrightarrow7x=35\)

\(\Leftrightarrow x=5\)

Đúng(1)

TM

Trần Minh Hiếu

25 tháng 12 2022

\(\left(5x-3\right)\left(x-2\right)=\left(x-1\right)\left(x-2\right)\)

\(\Leftrightarrow\left(5x-3\right)\left(x-2\right)-\left(x-1\right)\left(x-2\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(5x-3-x+1\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(4x+2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\4x+2=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{-1}{2}\end{matrix}\right.\)

Đúng(1)

DC

ĐInh Cao Quang Trung

10 tháng 11 2021

Tìm x biết: (x + 2)^2 - (x + 2)(x - 3) = 0

Tìm x biết :
a,(x+2)^2-(x+2)(x-3)=0
b,2x^3-4x^2+2x=0
c,(x-1)^2-(2x+1)^2=0

#Toán lớp 8

1

NH

Nguyễn Hoàng Minh

10 tháng 11 2021

\(a,\Leftrightarrow\left(x+2\right)\left(x+2-x+3\right)=0\\ \Leftrightarrow5\left(x+2\right)=0\Leftrightarrow x=-2\\ b,\Leftrightarrow2x\left(x-1\right)^2=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\\ c,\Leftrightarrow\left(x-1-2x-1\right)\left(x-1+2x+1\right)=0\\ \Leftrightarrow3x\left(-x-2\right)=0\Leftrightarrow-3x\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)

Đúng(1)

LM

Lục Mão Thiên

12 tháng 1 2020 - olm

Tìm x biết (1 - x)/(x^2 + x + 1) - (x - 1)/(x^2 - x + 1) = 3/[x.(x^4 + x^2 + 1)]

#Toán lớp 8

2

D

阮草~๖ۣۜDαɾƙ

12 tháng 1 2020

\(\frac{1-x}{x^2+x+1}-\frac{x-1}{x^2-x+1}=\frac{3}{\left[x\left(x^4+x^2+1\right)\right]}\)

\(\Leftrightarrow\frac{\left(1-x\right)x\left(x^2-x+1\right)\left(x^4+x^2+1\right)}{x\left(x^2+x+1\right)\left(x^2-x+1\right)\left(x^4+x^2+1\right)}\)\(-\)\(\frac{x\left(x-1\right)\left(x^2+x+1\right)\left(x^4+x^2+1\right)}{x\left(x^2+x+1\right)\left(x^2-x+1\right)\left(x^4+x^2+1\right)}\)\(=\)\(\frac{3\left(x^2-x+1\right)\left(x^2+x+1\right)}{x\left(x^2+x+1\right)\left(x^2-x+1\right)\left(x^4+x^2+1\right)}\)

\(\Rightarrow\left(1-x\right)x\left(x^2-x+1\right)\left(x^4+x^2+1\right)-x\left(x-1\right)\left(x^2+x+1\right)\left(x^4+x^2+1\right)=\)\(3\left(x^2-x+1\right)\left(x^2+x+1\right)\)

\(\Leftrightarrow\left(x-x^2\right)\left(x^2-x+1\right)\left(x^4+x^2+1\right)-\left(x^2-x\right)\left(x^2+x+1\right)\left(x^4+x^2+1\right)=\)\(\left(3x^2-3x+3\right)\left(x^2+x+1\right)\)

\(\Leftrightarrow\left(x^3-x^2+x-x^4+x^3-x^2\right)\left(x^4+x^2+1\right)-\left(x^4+x^3+x^2-x^3-x^2-x\right)\left(x^4+x^2+1\right)=\) \(3x^4+3x^3+3x^2-3x^3-3x^2-3x+3x^2+3x+3\)

\(\Leftrightarrow\left(2x^3-2x^2+x-x^4\right)\left(x^4+x^2+1\right)-\left(x^4-x\right)\left(x^4+x+1\right)=3x^4+3x^2+3\)

\(\Leftrightarrow\left(x^4+x^2+1\right)\left(2x^3-2x^2+x-x^4-x^4+x\right)=3x^4+3x^2+3\)

\(\Leftrightarrow\left(x^4+x^2+1\right)\left(2x^3-2x^2+2x-2x^4\right)=3x^4+3x^2+3\)

\(\Leftrightarrow2x^7-2x^6+2x^5-2x^8+2x^5-2x^4+2x^3-2x+2x^3-2x^2+2x-2x^4-3x^4-3x^2-3=0\)

\(\Leftrightarrow2x^7-2x^6+4x^5-2x^8-7x^4+x^2-3=0\)

Đến đây thì chịu òi :^ Sr nha

Đúng(2)

TP

Trần Phúc Khang

13 tháng 1 2020

\(\frac{1-x}{x^2+x+1}-\frac{x-1}{x^2-x+1}=\frac{3}{x\left(x^4+x^2+1\right)}\)

Ta có \(x^4+x^2+1=\left(x^2+1\right)^2-x^2=\left(x^2-x+1\right)\left(x^2+x+1\right)\)

=> \(\left(1-x\right)\left(\frac{1}{x^2+x+1}+\frac{1}{x^2-x+1}\right)=\frac{3}{x\left(x^4+x^2+1\right)}\)

<=>\(\left(1-x\right)\left(2x^2+2\right).x=3\)

Do \(2x^2+2>0\)

=> \(\left(1-x\right).x>0\)

=> \(0< x< 1\)=> \(2x^2+2< 4\)

Pt<=> \(\left(x-x^2\right)\left(2x^2+2\right)=3\)

Mà \(x-x^2\le\frac{1}{4};2x^2+2< 4\)

=> \(VT< 1\)

=> PT vô nghiệm

Đúng(0)

MG

mk gamevblc

6 tháng 4 2019 - olm

a,Tìm stn x,y biết:(2x+1)(y-3)=12

b,tìm stn x biết : 2^x+(2^x+1)+(2^x+2)+....+(2^x+2015)=(2^2019)-8

#Toán lớp 6

2

HH

Hoàng hôn ( Cool Team )

22 tháng 4 2020

(2x+1)(y-3)=12

Vì x;y là số tự nhiên => 2x+1;y-3 là số tự nhiên

=> 2x+1;y-3 E Ư(12)

Ta có bảng:

2x+1	1	12	3	4	2	6
y-3	12	1	4	3	6	2
x	0	11/2 (loại)	1	3/2(loại)	1/2(loại)	5/2(loại)
y	15	4	7	6	9	5

Vậy cặp số tự nhiên (x;y) cần tìm là: (0;15) ; (1;7)

Đúng(0)

JK

Jennie Kim

22 tháng 4 2020

(2x + 1)(y - 3) = 12

=> 2x + 1;y - 3 thuộc Ư(12)

vì x là stn => 2x + 1 là stn, ta có bảng

2x+1	1	12	2	6	3	4
y-3	12	1	6	2	4	3
x	0	loại	loại	loại	1	loại
y	15				7

Đúng(0)

TK

Tuấn Kiên Phạm

19 tháng 5 2022

Cho biểu thức \(A=\dfrac{x^2+x}{x^2-2x+1}:\left(\dfrac{x+1}{x}-\dfrac{1}{1-x}+\dfrac{2-x^2}{x^2-x}\right)\)a) Rút gọn \(A\)b) Tính \(A\) biết \(\left|x-3\right|=2\)c) Tìm \(x\) để \(A=\dfrac{1}{2}\)d) Tìm \(x\) để \(A>1\)e) Tìm \(x\) nguyên để \(A\) có giá trị nguyênf) Với \(x>1\). Tìm giá trị nhỏ nhất...

Đọc tiếp

#Toán lớp 8

2

NL

Nguyễn Lê Phước Thịnh

19 tháng 5 2022

a: \(E=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}:\left(\dfrac{x+1}{x}+\dfrac{1}{x-1}+\dfrac{2-x^2}{x\left(x-1\right)}\right)\)

\(=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}:\dfrac{x^2-1+x+2-x^2}{x\left(x-1\right)}\)

\(=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}\cdot\dfrac{x\left(x-1\right)}{x+1}=\dfrac{x^2}{x-1}\)

b: |x-3|=2

=>x-3=2 hoặc x-3=-2

=>x=5(nhận) hoặc x=1(loại)

Khi x=5 thì \(E=\dfrac{5^2}{5-1}=\dfrac{25}{4}\)

c: Để E=1/2 thì \(\dfrac{x^2}{x-1}=\dfrac{1}{2}\)

\(\Leftrightarrow2x^2-x+1=0\)

hay \(x\in\varnothing\)

Đúng(3)

TT

Trần Tuấn Hoàng

19 tháng 5 2022

f) \(A=\dfrac{x^2}{x-1}=\dfrac{x^2-x+x-1+1}{x-1}=\dfrac{x\left(x-1\right)+x-1+1}{x-1}=x+1+\dfrac{1}{x-1}=x-1+\dfrac{1}{x-1}+2\ge2\sqrt{\left(x-1\right).\dfrac{1}{x-1}}+2=4\)\(A=4\Leftrightarrow x=2\)

-Vậy \(A_{min}=4\)

Đúng(1)

HC

Hùng Chu

21 tháng 6 2021

Cho biểu thức C =( \(\dfrac{2x^2+1}{x^3-1}-\dfrac{1}{x-1}\)):(1-\(\dfrac{x^2-2}{x^2+x+1}\))

a) Rút gọn C

b) Tính giá trị của C biết |1-x| +2 =3(x+1)

c) Tìm x nguyên để C nguyên

d) Tìm x biết |C| > C

e) Tìm x để C²-C + 1 đạt giá trị nhỏ nhất

#Toán lớp 8

1

HT

Huỳnh Thị Thanh Ngân

21 tháng 6 2021

\(C=\left(\dfrac{2x^2+1}{x^3-1}-\dfrac{1}{x-1}\right)\div\left(1-\dfrac{x^2-2}{x^2+x+1}\right)\)

ĐKXĐ: \(x\ne1\)

\(C=[\left(\dfrac{2x^2+1}{(x-1)\left(x^2+x+1\right)}-\dfrac{1}{x-1}\right)]\div\left(1-\dfrac{x^2-2}{x^2+x+1}\right)\)

\(\Leftrightarrow C=[\left(\dfrac{2x^2+1}{(x-1)\left(x^2+x+1\right)}-\dfrac{1\left(x^2+x+1\right)}{(x-1)\left(x^2+x+1\right)}\right)]\div[\dfrac{(x-1)\left(x^2+x+1\right)}{(x-1)\left(x^2+x+1\right)}-\dfrac{(x^2-2)(x-1)}{(x^2+x+1)\left(x-1\right)}]\)

\(\Rightarrow C=\left[2x^2+1-1\left(x^2+x+1\right)\right]\div\left[\left(x-1\right)\left(x^2+x+1\right)-\left(x-1\right)\left(x^2-2\right)\right]\)

\(\Rightarrow C=(2x^2+1-x^2-x-1)\div\left[\left(x-1\right)\left(x^2+x+1-x^2+2\right)\right]\)

\(\Rightarrow C=\left(x^2-x\right)\div\left[\left(x-1\right)\left(x+3\right)\right]\)

Đúng(2)

E

êrgsrgrg

24 tháng 9 2021

: Tìm x biết

a) (x + 1)³x – x( x -2)² + x -1 = 0

b) ( x – 2)³ – x²(x -6) =4

c) ( x -1)( x² + x + 1) – x( x+2)(x -2) =5

d) 3(x -1)² – 3x( x -5) =1

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

24 tháng 9 2021

b: Ta có: \(\left(x-2\right)^3-x^2\left(x-6\right)=4\)

\(\Leftrightarrow x^3-6x^2+12x-8-x^3+6x^2=4\)

\(\Leftrightarrow12x=12\)

hay x=2

d: Ta có: \(3\left(x-1\right)^2-3x\left(x-5\right)=1\)

\(\Leftrightarrow3x^2-6x+3-3x^2+15x=1\)

\(\Leftrightarrow9x=-2\)

hay \(x=-\dfrac{2}{9}\)

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP