Cho hình chóp S.ABC có S A = 8 , SA vuông góc với đáy. Tam giác ABC vuông tại A, B C = 7 . Tính bán kính của mặt cầu ngoại tiếp khối chóp.
A. 113
B. 113 4
C. 113 3
D. 113 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 6 2017
Đáp án D
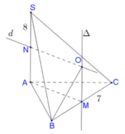
Gọi M là trung điểm của BC. Suy ra M là tâm đường tròn ngoại tiếp tam giác vuông ABC.
Kẻ đường thẳng Δ đi qua M và vuông góc với mặt phẳng (ABC), Δ chính là trục của đường tròn ngoại tiếp đa giác đáy.
Trong mặt phẳng chứa SA và Δ, dựng đường trung trực d của
CM
24 tháng 5 2019
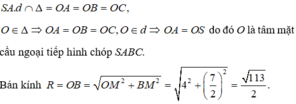
Ta có S A ⊥ A B C A C ⊂ A B C
⇒ S A ⊥ A C
S A ⊥ A B C A B ⊥ B C
⇒ S B ⊥ B C . Tâm I của mặt cầu là trung điểm của cạnh huyền SC.
Bán kính: R = SI = S C 2
S A 2 + A C 2 2 = a 2 + a 2 + a 2 2 = a 3 2
Đáp án D
Đáp án D
Gọi M là trung điểm của BC. Suy ra M là tâm đường tròn ngoại tiếp tam giác vuông ABC. Kẻ đường thẳng D đi qua M và vuông góc với mặt phẳng (ABC), D chính là trục của đường tròn ngoại tiếp đa giác đáy.
Trong mặt phẳng chứa SA và D, dựng đường trung trực d của SA. d ∩ D = O
do đó O là tâm mặt cầu ngoại tiếp hình chóp SABC