Xét tam giác ABC vuông tại A có ∠B = α. Chứng minh rằng
a ) α = 45 ° ⇔ AC AB = 1 b ) α = 60 ° ⇔ AC AB = 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

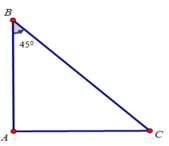
Tam giác ABC vuông tại A có ∠B = 45o ⇒ΔABC vuông cân tại A
⇒AB = AC ⇒AB/AC = 1

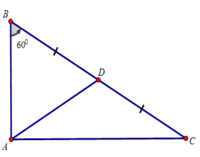
Kẻ trung tuyến AD của tam giác vuông ABC
⇒ AD = BD = BC/2
Tam giác ABD có: AD = BD, ∠(ABD) = 60o
⇒ ΔABD là tam giác đều
⇒ AB = AD = BC/2 ⇒ BC = AB
Áp dụng định lí Pytago vào tam giác ABC vuông tại A có:
AB2 + AC2 = BC2
⇔ AB2 + AC2 = 4 AB2
⇔ AC2 = 3 AB2 ⇔ AC = √3 AB
⇔ AC/AB = √3

ta có: B=\(\alpha\) mà \(\frac{AC}{AB}=\sqrt{3}\)→\(\tan\alpha=\sqrt{3}\)
lại có: 1+ tan2\(\alpha\)=\(\frac{1}{\cos^2\alpha}\)→cos2\(\alpha\)=\(\frac{1}{4}\)→cos \(\alpha\)=\(\frac{1}{2}\)hay \(\frac{AB}{BC}=\frac{1}{2}\)
→ C=30o(Δ vuông có 1 cạnh góc vuông = 1/2 cạnh huyền)
do đó B=600

Góc 2α = A M H ^
a, Ta có: sin 2 α = A H A M = 2 A H A M = 2 A B . A C B C 2 = 2 sin α . cos α
b, 1 + cos2α = 1 + H M A M = H C A M = 2 H C B C = 2 . A C 2 B C 2 = 2 cos 2 α
c, 1 – cos2α = 1 - H M A M = H B A M = 2 H B B C = 2 . A B 2 B C 2 = 2 sin 2 α

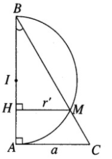
Tam giác vuông ABC có BC = 2a và AC = a nên ta suy ra ∠ ABC = 30 ° . Khi quay xung quanh trục AB cạnh BC tạo nên mặt nón tròn xoay có góc ở đỉnh bằng 60 ° và có đường tròn đáy có bán kính AC = a. Khi xoay xung quanh trục AB nửa đường tròn đường kính AB tạo nên mặt cầu có tâm là trung điểm I để đoạn AB và bán kính r = AB/2.
a)
Tam giác ABC vuông tại A có ∠B = 45o ⇒ΔABC vuông cân tại A
⇒AB = AC ⇒AB/AC = 1
b)
Kẻ trung tuyến AD của tam giác vuông ABC
⇒ AD = BD = BC/2
Tam giác ABD có: AD = BD, ∠(ABD) = 60o
⇒ ΔABD là tam giác đều
⇒ AB = AD = BC/2 ⇒ BC = AB
Áp dụng định lí Pytago vào tam giác ABC vuông tại A có:
AB2 + AC2 = BC2
⇔ AB2 + AC2 = 4 AB2
⇔ AC2 = 3 AB2 ⇔ AC = √3 AB
⇔ AC/AB = √3