Question

[Pham Trong Bach]

Cho x O y ^ = 120°. Ở phía ngoài của góc vẽ hai tia Oc và Od sao cho Od ⊥  Ox và Oc  ⊥ Oy. Gọi Om và On theo thứ tự là phân giác của  x O y ^  và d O c ^ ; Oy' là tia đối của tia Oy. Chứng minh:

a) Ox là tia phân giác của y ' O m ^ ;

 b) Oy' nằm giữa hai tia Ox và Od;

c) Góc mOn là góc bẹt

Answer 1

[Cao Minh Tâm]

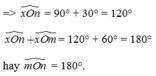
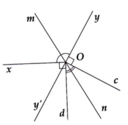
a) Có x O m ^ = y O m ^  = 60°

=> y O m ^ < y O x ^ < y O y ' ^

=>Tia Ox nằm giữa Om và Oy'

Lại có:

  y ' O x ^ = 180°- 120° = 60° =   x O m ^

=> Ox là phân giác của  y ' O m ^ .

b)   x O y ' ^ < x O d ^ suy ra tia Oy' nằm giữa hai tia Ox và Od.

c)   y O d ^ = 90° - 60° = 30°

  c O d ^ = c O y ' ^ − y ' O d ^ = 90°- 30° = 60° =>  d O n ^  = 30°

=> x O n ^  = 90° + 30° = 120°

x O n ^ + x O m ^ = 120° + 60° = 180° hay   m O n ^ = 180°.