Cho tam giác DEF cân tại D, các đường cao EM, FN cắt nhau tại O. Gọi I là giao điểm của DO với EF. Chứng minh IE = IF.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LH
10 tháng 5 2021
b, Vì K thuộc đường tròn ngoại tiếp tam giác DEF nên tứ giác DKEF nội tiếp
→PKE = PFD (góc ngoài tứ giác)
mà DPF chung
→ΔPKE đồng dạng ΔPFD (góc-góc)
→\(\dfrac{PK}{PE}=\dfrac{PF}{PD}\)
→PK.PD=PF.PE (1)
Vì tứ giác NMFE là tứ giác nội tiếp
→PNE =PFD
mà MPF chung
→ΔPNE đồng dạng ΔPFM (góc-góc)
→\(\dfrac{PN}{PE}=\dfrac{PF}{PM}\) (2 góc tương ứng)
→PN.PM=PE.PF (2)
Từ (1) và (2) suy ra:PN.PM=PK.PD(đpcm)
10 tháng 5 2021
c) Mình ghi có hơi gọn tí ở một số bước (do đây là những bài toán cơ bản, có thể tự chứng minh được), bạn thông cảm nha!
ENMF nội tiếp và DNHM nội tiếp
\(\Rightarrow PE.PF=PN.PM=PK.PD\) hay \(PN.PM=PK.PD \Rightarrow \) DKNM nội tiếp
\(\Rightarrow\) DKNHM nội tiếp hay DKHM nội tiếp
\(\Rightarrow \widehat{DKH}=180^{\circ}-\widehat{DMH}=180^{\circ}-90^{\circ}=90^{\circ}\) hay \(HK \perp PD\)
Kẻ đường kính DA của đường tròn ngoại tiếp \(\Delta DEF\)
\(\Rightarrow\) EHFA là hình bình hành (bài toán quen thuộc)
Hay H, Q, A thẳng hàng
\(\Delta AKD\) nội tiếp đường tròn đường kính AD nên tam giác này vuông tại K
\(\Rightarrow AK\perp PD\) mà \(HK \perp PD\)
\(\Rightarrow \) A, H, K thẳng hàng mà H, Q, A thẳng hàng
\(\Rightarrow\) Q, H, K thẳng hàng
\(\Rightarrow QK \perp PD\) mà \(DH \perp PQ\)
\(\Rightarrow PH \perp DQ (đpcm)\)
1 tháng 3 2022
1: Ta có: ΔDEF cân tại D
mà DH là đường cao
nên H là trung điểm của FE
hay HE=HF
EF=8cm
nên HE=4cm
=>DH=3cm
2: Xét ΔDEM và ΔDFN có
DE=DF
\(\widehat{EDM}\) chung
DM=DN
Do đó: ΔDEM=ΔDFN
Suy ra: EM=FN
3: Xét ΔNEF và ΔMFE có
NE=MF
\(\widehat{NEF}=\widehat{MFE}\)
FE chung
Do đó:ΔNEF=ΔMFE
Suy ra: \(\widehat{KFE}=\widehat{KEF}\)
=>ΔKEF cân tại K
hay KE=KF
4: Ta có: DE=DF
nên D nằm trên đường trung trực của EF(1)
ta có: KE=KF
nên K nằm trên đường trung trực của EF(2)
ta có: HE=HF
nên H nằm trên đường trung trực của EF(3)
Từ (1), (2) và (3) suy ra D,K,H thẳng hàng
5 tháng 11 2023
\({}\)
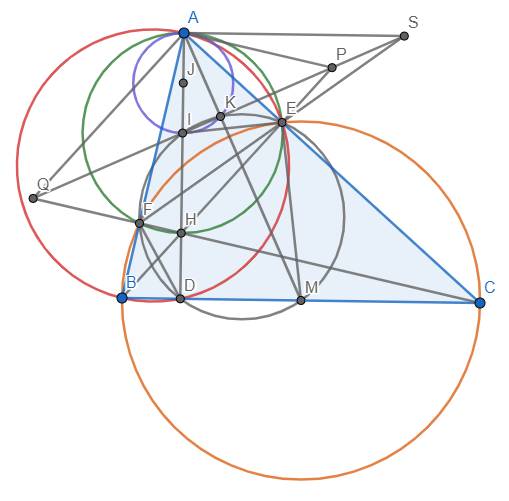
a) Vì \(\widehat{BEC}=\widehat{BFC}=90^o\) nên tứ giác BEFC nội tiếp đường tròn đường kính BC. Tương tự như thế, tứ giác AEDB nội tiếp đường tròn đường kính AB. Cũng có \(\widehat{AEH}=\widehat{AFH}=90^o\) nên tứ giác AEHF nội tiếp đường tròn đường kính AH.
Ta có \(\widehat{IEM}=\widehat{IEB}+\widehat{BEM}\)
\(=\left(90^o-\widehat{IEA}\right)+\widehat{EBC}\)
\(=90^o-\widehat{EAD}+\widehat{EBD}=90^o\) (do \(\widehat{EBD}=\widehat{EAD}\))
Vậy \(IE\perp ME\)
b) Dễ thấy các điểm I, D, E, F, M, K cùng thuộc đường tròn đường kính IM. Gọi J là trung điểm AI thì I chính là tâm của đường tròn (AIK) nên (J) tiếp xúc với (I) tại A. Dẫn đến A nằm trên trục đẳng phương của (I) và (J)
Mặt khác, ta có \(SK.SI=SE.SF\) nên \(P_{S/\left(I\right)}=P_{S/\left(J\right)}\) hay S nằm trên trục đẳng phương của (I) và (J). Suy ra AS là trục đẳng phương của (I) và (J). \(\Rightarrow\)\(AS\perp IJ\) hay AS//BC (đpcm).
c) Ta thấy tứ giác AKEP nội tiếp đường tròn AP
\(\Rightarrow\widehat{APB}=\widehat{MKE}=\widehat{MDE}=\widehat{BAC}\)
\(\Rightarrow\Delta BAE~\Delta BPA\left(g.g\right)\Rightarrow\widehat{BAP}=\widehat{BEA}=90^o\)
\(\Rightarrow\) AP//QH \(\left(\perp AB\right)\)
\(\Rightarrow\widehat{IAP}=\widehat{IHQ}\) (2 góc so le trong)
Từ đó dễ dàng chứng minh \(\Delta IAP=\Delta IHQ\left(g.c.g\right)\) \(\Rightarrow IP=IQ\) hay I là trung điểm PQ (đpcm)
LK
3 tháng 3 2018
a) XÉT \(\Delta DEM\)VÀ \(\Delta DEN\)
^D CHUNG
DM=DN \(\Rightarrow\Delta DEM=\Delta DEN\left(C-G-C\right)\)=> ^DEM=^DEN
DF=DE
b) VÌ ^DEF=^DFE MÀ ^DEM=^DEN =>^IEF=^IFE \(\Rightarrow\Delta IEF\)CÂN
c) TA CÓ \(\Delta DNM\)CÂN TẠI D NÊN ^DMN=^DNM=\(\frac{180^0-D}{2}\)(1)
TA LẠI CÓ \(\Delta DÈF\)CÂN TẠI D NÊN ^DEF=^DFE=\(\frac{180^0-D}{2}\)(2)
TỪ (1) VÀ (2) => ^DMN=^DFE
MÀ 2 GÓC NÀY Ở VỊ TRÍ ĐỒNG VỊ NÊN NM // EF
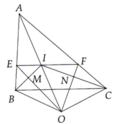
Chứng minh được AI là đường trung tuyến của tam giác ABC, từ đó IE = IF.