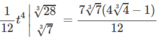∫ 1 2 3 x 3 + 4 3 x 2 d x (đặt t = 3 x 3 + 4 3 )
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TH
2 tháng 8 2019
mình k hiểu đề bài 2 câu a và b, bạn viết lại nhé!
c) C = (2x-1)(x-1)(x-3)(2x+3) +9
= ( 2x2 -x -2x +1 )( 2x2 -6x +3x -9) + 9
= (2x2 -3x +3 )( 2x2 -3x -9) +9
đặt 2x2 - 3x -3 = t
=> C = (t +6 )( t - 6) +9
= t2 -36 + 9 = t2 - 27
= \(\left(t-3\sqrt{3}\right)\left(t+3\sqrt{3}\right)\)
= \(\left(2x^2-3x-3-3\sqrt{3}\right)\left(2x^2-3x-3+3\sqrt{3}\right)\)
d) D = (4x + 1)(12x - 1)(3x + 2)(x + 1) - 4
= (12x2 + 11x +2)(12x2 +11x - 1) - 4
đặt 12x2 + 11x = t
=> D = (t + 2)(t - 1) - 4
= t2 + t - 6 = (t - 2)(t + 3)
=> D = (12x2 + 11x - 2)(12x2 + 11x + 3)
25 tháng 9 2021
a) \(\left(x+1\right)\left(x+2\right)\left(x+4\right)\left(x+5\right)-4=\left(x^2+6x+5\right)\left(x^2+6x+8\right)-4\)
Đặt \(t=x^2+6x+5\)
\(PT=t\left(t+3\right)-4=t^2+3t-4=\left(t-1\right)\left(t+4\right)\)
Thay t: \(PT=\left(x^2+6x+5-1\right)\left(x^2+6x+5+4\right)=\left(x^2+6x+4\right)\left(x^2+6x+9\right)=\left(x^2+6x+4\right)\left(x+3\right)^2\)
b) Đặt \(t=\left(2x+1\right)^2\)
\(PT=t^2-3t+2=\left(t^2-3t+\dfrac{9}{4}\right)-\dfrac{1}{4}=\left(t+\dfrac{3}{2}\right)^2-\dfrac{1}{4}=\left(t+1\right)\left(t+2\right)\)
Thay t:
\(PT=\left[\left(2x+1\right)^2+1\right]\left[\left(2x+1\right)^2+2\right]=\left[4x^2+4x+2\right]\left[4x^2+4x+3\right]=2\left[2x^2+2x+1\right]\left[4x^2+4x+3\right]\)
DH
31 tháng 8 2019
a, \(\left(x+1\right)^2=169\)
\(\left(x+1\right)^2=13^2\)
\(x+1=13\)
\(x=13-1\)
\(x=12\)
VM
31 tháng 8 2019
1.
a) \(\left(x+1\right)^2=169\)
⇒ \(x+1=\pm13\)
⇒ \(\left[{}\begin{matrix}x+1=13\\x+1=-13\end{matrix}\right.\) ⇒ \(\left[{}\begin{matrix}x=13-1\\x=\left(-13\right)-1\end{matrix}\right.\) ⇒ \(\left[{}\begin{matrix}x=12\\x=-14\end{matrix}\right.\)
Vậy \(x\in\left\{12;-14\right\}.\)
b) \(\left(x+3\right)^3=-\frac{1}{27}\)
⇒ \(\left(x+3\right)^3=\left(-\frac{1}{3}\right)^3\)
⇒ \(x+3=-\frac{1}{3}\)
⇒ \(x=\left(-\frac{1}{3}\right)-3\)
⇒ \(x=-\frac{10}{3}\)
Vậy \(x=-\frac{10}{3}.\)
c) \(\left(2x-4\right)^4=\frac{1}{625}\)
⇒ \(2x-4=\pm\frac{1}{5}\)
⇒ \(\left[{}\begin{matrix}2x-4=\frac{1}{5}\\2x-4=-\frac{1}{5}\end{matrix}\right.\) ⇒ \(\left[{}\begin{matrix}2x=\frac{1}{5}+4=\frac{21}{5}\\2x=\left(-\frac{1}{5}\right)+4=\frac{19}{5}\end{matrix}\right.\) ⇒ \(\left[{}\begin{matrix}x=\frac{21}{5}:2\\x=\frac{19}{5}:2\end{matrix}\right.\)
⇒ \(\left[{}\begin{matrix}x=\frac{21}{10}\\x=\frac{19}{10}\end{matrix}\right.\)
Vậy \(x\in\left\{\frac{21}{10};\frac{19}{10}\right\}.\)
Còn câu d) bạn làm tương tự như mấy câu trên.
Chúc bạn học tốt!
2 tháng 9 2020
Bài 1:
a) Ta có: \(A=\left(x+3\right)^2+\left(x-3\right)\left(x+3\right)-2\left(x+2\right)\left(x-4\right)\)
\(=x^2+6x+9+x^2-9-2\left(x^2-4x+2x-8\right)\)
\(=2x^2+6x-2\left(x^2-2x-8\right)\)
\(=2x^2+6x-2x^2+4x+16\)
\(=10x+16\)
Thay \(x=\frac{1}{2}\) vào biểu thức \(A=10x+16\), ta được:
\(A=10\cdot\frac{1}{2}+16=5+16=21\)
Vậy: 21 là giá trị của biểu thức \(A=\left(x+3\right)^2+\left(x-3\right)\left(x+3\right)-2\left(x+2\right)\left(x-4\right)\) tại \(x=\frac{1}{2}\)
b) Ta có: \(B=\left(3x+4\right)^2-\left(x+4\right)\left(x+4\right)-10x\)
\(=9x^2+24x+16-\left(x^2+8x+16\right)-10x\)
\(=9x^2+24x+16-x^2-8x-16-10x\)
\(=8x^2+6x\)
Thay \(x=\frac{1}{10}\) vào biểu thức \(B=8x^2+6x\), ta được:
\(B=8\cdot\left(\frac{1}{10}\right)^2+6\cdot\frac{1}{10}=8\cdot\frac{1}{100}+\frac{6}{10}\)
\(=\frac{8}{100}+\frac{6}{10}\)
\(=\frac{8}{100}+\frac{60}{100}=\frac{17}{25}\)
Vậy: \(\frac{17}{25}\) là giá trị của biểu thức \(B=\left(3x+4\right)^2-\left(x+4\right)\left(x+4\right)-10x\) tại \(x=\frac{1}{10}\)
c) Ta có: \(C=\left(x+1\right)^2-\left(2x-1\right)^2+3\left(x-2\right)\left(x+2\right)\)
\(=x^2+2x+1-\left(4x^2-4x+1\right)+3\left(x^2-4\right)\)
\(=x^2+2x+1-4x^2+4x-1+3x^2-12\)
\(=6x-12\)
Thay x=1 vào biểu thức C=6x-12, ta được:
\(C=6\cdot1-12=6-12=-6\)
Vậy: -6 là giá trị của biểu thức \(C=\left(x+1\right)^2-\left(2x-1\right)^2+3\left(x-2\right)\left(x+2\right)\) tại x=1
d) Ta có: \(D=\left(x-3\right)\left(x+3\right)+\left(x-2\right)^2-2x\left(x-4\right)\)
\(=x^2-9+x^2-4x+4-2x^2+8x\)
\(=4x-5\)
Thay x=-1 vào biểu thức D=4x-5,ta được:
\(D=4\cdot\left(-1\right)-5=-4-5=-9\)
Vậy: -9 là giá trị của biểu thức \(D=\left(x-3\right)\left(x+3\right)+\left(x-2\right)^2-2x\left(x-4\right)\) tại x=-1
20 tháng 7 2020
a) Ta có: \(A=\left(x+3\right)^2+\left(x-3\right)\left(x+3\right)-2\left(x+2\right)\left(x-4\right)\)
\(=x^2+6x+9+x^2-9-2\left(x^2-2x-8\right)\)
\(=2x^2+6x-2x^2+4x+16\)
\(=10x+16\)
Thay \(x=-\frac{1}{2}\) vào biểu thức \(A=10x+16\), ta được:
\(A=10\cdot\frac{-1}{2}+16=-5+16=11\)
Vậy: 11 là giá trị của biểu thức \(A=\left(x+3\right)^2+\left(x-3\right)\left(x+3\right)-2\left(x+2\right)\left(x-4\right)\) tại \(x=-\frac{1}{2}\)
b) Ta có: \(B=\left(3x+4\right)^2-\left(x-4\right)\left(x+4\right)-10x\)
\(=9x^2+24x+16-\left(x^2-16\right)-10x\)
\(=9x^2+14x+16-x^2+16\)
\(=8x^2+14x+32\)
Thay \(x=-\frac{1}{10}\) vào biểu thức \(B=8x^2+14x+32\), ta được:
\(B=8\cdot\left(-\frac{1}{10}\right)^2+14\cdot\frac{-1}{10}+32\)
\(=8\cdot\frac{1}{100}-\frac{14}{10}+32\)
\(=\frac{2}{25}-\frac{14}{10}+32\)
\(=\frac{4}{50}-\frac{70}{50}+\frac{1600}{50}\)
\(=\frac{1534}{50}\)
Vậy: \(\frac{1534}{50}\) là giá trị của biểu thức \(B=\left(3x+4\right)^2-\left(x-4\right)\left(x+4\right)-10x\) tại \(x=-\frac{1}{10}\)
c) Ta có: \(C=\left(x+1\right)^2-\left(2x-1\right)^2+3\left(x-2\right)\left(x+2\right)\)
\(=x^2+2x+1-\left(4x^2-4x+1\right)+3\left(x^2-4\right)\)
\(=x^2+2x+1-4x^2+4x-1+3x^2-12\)
\(=6x-12\)
Thay x=1 vào biểu thức C=6x-12, ta được:
\(C=6\cdot1-12=6-12=-6\)
Vậy: -6 là giá trị của biểu thức \(C=\left(x+1\right)^2-\left(2x-1\right)^2+3\left(x-2\right)\left(x+2\right)\) tại x=1
d) Ta có: \(D=\left(x-3\right)\left(x+3\right)+\left(x-2\right)^2-2x\left(x-4\right)\)
\(=x^2-9+x^2-4x+4-2x^2+8x\)
\(=4x-5\)
Thay x=-1 vào biểu thức D=4x-5, ta được:
\(D=4\cdot\left(-1\right)-5=-4-5=-9\)
Vậy: -9 là giá trị của biểu thức \(D=\left(x-3\right)\left(x+3\right)+\left(x-2\right)^2-2x\left(x-4\right)\) tại x=-1
Đổi biến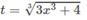
Đáp án: