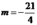Cho phương trình 2 x + m = 3 x − 2 . Tìm giá trị của tham số m để phương trình có nghiệm x = 4.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 5 2021
1) điều kiện của m: m khác 5/2
thế x=2 vào pt1 ta đc:
(2m-5)*4 - 4(m-1)+3=0 <=> 8m-20-4m+4+3=0<=> 4m = 13 <=> m=13/4 (nhận)
lập △'=[-(m-1)]2-*(2m-5)*3 = (m-4)2
vì (m-4)2 ≥ 0 nên phương trình có nghiệm kép => x1= x2 =2
3) vì △'≥0 với mọi m nên phương trình đã cho có nghiệm với mọi m
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 12 2020
1.
Đặt \(\sqrt{x^2-4x+5}=t\ge1\Rightarrow x^2-4x=t^2-5\)
Pt trở thành:
\(4t=t^2-5+2m-1\)
\(\Leftrightarrow t^2-4t+2m-6=0\) (1)
Pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm pb đều lớn hơn 1
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=4-\left(2m-6\right)>0\\\left(t_1-1\right)\left(t_2-1\right)>0\\\dfrac{t_1+t_2}{2}>1\\\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}10-2m>0\\t_1t_2-\left(t_1+t_1\right)+1>0\\t_1+t_2>2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 5\\2m-6-4+1>0\\4>2\end{matrix}\right.\) \(\Leftrightarrow\dfrac{9}{2}< m< 5\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 12 2020
2.
Để pt đã cho có 2 nghiệm:
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\\Delta'=1+4\left(m-3\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\m\ge\dfrac{11}{4}\end{matrix}\right.\)
Khi đó:
\(x_1^2+x_2^2=4\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\)
\(\Leftrightarrow\dfrac{4}{\left(m-3\right)^2}+\dfrac{8}{m-3}=4\)
\(\Leftrightarrow\dfrac{1}{\left(m-3\right)^2}+\dfrac{2}{m-3}-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{m-3}=-1-\sqrt{2}\\\dfrac{1}{m-3}=-1+\sqrt{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=4-\sqrt{2}< \dfrac{11}{4}\left(loại\right)\\m=4+\sqrt{2}\end{matrix}\right.\)
H9
HT.Phong (9A5)
CTVHS
16 tháng 1
Ta có pt: \(mx^2-3\left(m+1\right)x+m^2-13m-4=0\)
Do pt có nghiệm là x = -2 nên thay vào pt ta có:
\(m\cdot\left(-2\right)^2-3\left(m+1\right)\cdot-2+m^2-13m-4=0\)
\(\Leftrightarrow4m+6\left(m+1\right)+m^2-13m-4=0\)
\(\Leftrightarrow6m+6+m^2-9m-4=0\)
\(\Leftrightarrow m^2-3m+2=0\)
\(\Delta=\left(-3\right)^2-4\cdot1\cdot2=1>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m_1=\dfrac{3+\sqrt{1}}{2}=2\\m_2=\dfrac{3-\sqrt{1}}{2}=1\end{matrix}\right.\)
Nếu m = 1 thì pt là:
\(x^2-3\left(1+1\right)x+1^2-13\cdot1-4=0\)
\(\Leftrightarrow x^2-6x-16=0\)
Theo vi-et: \(x_1+x_2=-\dfrac{-6}{1}\Rightarrow x_2=6-x_2=8\)
Nếu m = 2 thì pt là:
\(2x^2-3\cdot\left(2+1\right)x+2^2-13\cdot2-4=0\)
\(\Leftrightarrow2x^2-9x-26=0\)
Theo vi-et: \(x_1+x_2=-\dfrac{-9}{2}\Leftrightarrow x_2=\dfrac{9}{2}+2=\dfrac{13}{2}\)
25 tháng 7 2023
a) Điều kiện để phương trình có hai nghiệm trái dấu là :
\(\left\{{}\begin{matrix}m\ne0\\\Delta phẩy>0\\x_1.x_2< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\m^2+4m+4-m^2+3m>0\\\dfrac{m-3}{m}< 0\end{matrix}\right.\)
\(\Rightarrow0< m< 3\)
b) Để phương trình có 2 nghiệm phân biệt thì : \(\Delta\) phẩy > 0
\(\Rightarrow m< 4\)
Ta có : \(\dfrac{1}{x_1^2}+\dfrac{1}{x_2^2}=2\)
\(\Leftrightarrow x_1^2+x_2^2=2x_1^2.x_2^2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1.x_2=2x_1^2.x_2^2\)
Theo Vi-ét ta có : \(x_1+x_2=\dfrac{-2\left(m-2\right)}{m};x_1.x_2=\dfrac{m-3}{m}\)
\(\Rightarrow\dfrac{4\left(m-2\right)^2}{m^2}-2.\dfrac{m-3}{m}=2.\dfrac{\left(m-3\right)^2}{m^2}\)
\(\Leftrightarrow m=1\left(tm\right)\)
Vậy...........
25 tháng 7 2023
a) \(mx^2+2\left(m-2\right)x+m-3=0\left(1\right)\)
Để \(\left(1\right)\) có hai nghiệm trái dấu \(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=\left(m-2\right)^2-m\left(m-3\right)>0\\\dfrac{m-3}{m}< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-4m+4-m^2-3m>0\\0< m< 3\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}7m+4>0\\0< m< 3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>-\dfrac{4}{7}\\0< m< 3\end{matrix}\right.\) \(\Leftrightarrow0< m< 3\)
b) \(\dfrac{1}{x^2_1}+\dfrac{1}{x^2_2}=2\Leftrightarrow\dfrac{x^2_1+x_2^2}{x^2_1.x^2_2}=2\) \(\Leftrightarrow\dfrac{\left(x_1+x_2\right)^2-4x_1.x_2}{x^2_1.x^2_2}=2\)
\(\Leftrightarrow\left(\dfrac{x_1+x_2}{x_1.x_2}\right)^2-\dfrac{4}{x_1.x_2}=2\)
\(\Leftrightarrow\left(\dfrac{\dfrac{2\left(2-m\right)}{m}}{\dfrac{m-3}{m}}\right)^2-\dfrac{4}{\dfrac{m-3}{m}}=2\)
\(\Leftrightarrow\left(\dfrac{2\left(2-m\right)}{m-3}\right)^2-\dfrac{4m}{m-3}=2\)
\(\Leftrightarrow4\left(2-m\right)^2-4m\left(m-3\right)=2.\left(m-3\right)^2\)
\(\Leftrightarrow4\left(4-4m+m^2\right)-4m^2+12=2.\left(m^2-6m+9\right)\)
\(\Leftrightarrow16-16m+4m^2-4m^2+12=2m^2-12m+18\)
\(\Leftrightarrow2m^2+4m-10=0\)
\(\Leftrightarrow m^2+2m-5=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-1+\sqrt[]{6}\\m=-1-\sqrt[]{6}\end{matrix}\right.\) \(\Leftrightarrow m=-1+\sqrt[]{6}\left(\Delta>0\Rightarrow m>-\dfrac{4}{7}\right)\)
AH
Akai Haruma
Giáo viên
30 tháng 4 2022
Bạn cần viết đề bằng công thức toán ( biểu tượng $\sum$ góc trái khung soạn thảo) để được hỗ trợ tốt hơn.
10 tháng 4 2021
a, Thay m = -1 vào phương trình trên ta được
\(x^2+4x-5=0\)
Ta có : \(\Delta=16+20=36\)
\(x_1=\frac{-4-6}{2}=-5;x_2=\frac{-4+6}{2}=1\)
Vậy với m = -1 thì x = -5 ; x = 1
b, Vì x = 2 là nghiệm của phương trình trên nên thay x = 2 vào phương trình trên ta được :
\(4+8+3m-2=0\Leftrightarrow3m=-10\Leftrightarrow m=-\frac{10}{3}\)
Vậy với x = 2 thì m = -10/3
c, Để phương trình có 2 nghiệm phân biệt thì \(\Delta>0\)hay
\(16-4\left(3m-2\right)=16-12m+8=4m+8>0\)
\(\Leftrightarrow8>-4m\Leftrightarrow m>-2\)
Theo Vi et ta có : \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=-4\\x_1x_2=\frac{c}{a}=3m-2\end{cases}}\)
\(\Leftrightarrow x_1+x_2=-4\Leftrightarrow x_1=-4-x_2\)(1)
suy ra : \(-4-x_2+2x_2=1\Leftrightarrow-4+x_2=1\Leftrightarrow x_2=5\)
Thay vào (1) ta được : \(x_1=-4-5=-9\)
Mà \(x_1x_2=3m-2\Rightarrow3m-2=-45\Leftrightarrow3m=-43\Leftrightarrow m=-\frac{43}{3}\)
RH
4 tháng 2
Đặt \(t=2^x>0\).
Phương trình ban đầu trở thành: \(t^2-4t+m=0\) (*)
Để phương trình ban đầu có 2 nghiệm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt dương:
\(\left\{{}\begin{matrix}\Delta'>0\\t_1+t_2>0\\t_1t_2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4-m>0\\4>0\left(đúng\right)\\m>0\end{matrix}\right.\Leftrightarrow0< m< 4\)
Y
12 tháng 3 2023
\(\left\{{}\begin{matrix}m\left(x+3\right)\le x+5\\m\left(x+2\right)\ge x+3\end{matrix}\right.\) có nghiệm chung \(\left(1\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\le\dfrac{x+5}{x+3}\\m\ge\dfrac{x+3}{x+2}\end{matrix}\right.\)
Để 2 pt có 1 nghệm chung thì \(\dfrac{x+5}{x+3}=\dfrac{x+3}{x+2}\)
\(\Leftrightarrow\left(x+5\right)\left(x+2\right)-\left(x+3\right)^2=0\)
\(\Leftrightarrow x^2+7x+10-x^2-6x-9=0\)
\(\Leftrightarrow x+1=0\)
\(\Leftrightarrow x=-1\)
Thay \(x=-1\) vào \(\left(1\right):\)
\(\left\{{}\begin{matrix}m\left(-1+3\right)\le-1+5\\m\left(-1+2\right)\ge-1+3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2m\le4\\m\ge2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\le2\\m\ge2\end{matrix}\right.\)
\(\Rightarrow m=2\)
Vậy m = 2 thì bpt trên có nghiệm chung
Thay x = 4 vào phương trình ta có: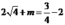
Từ đó tìm được