Cho hình thoi ABCD có cạnh AB cố định. Gọi O là trung điểm của AB, P là giao điểm của CO và BD. Chứng minh P chạy trên một đường tròn khi C, D thay đổi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Nhận xét
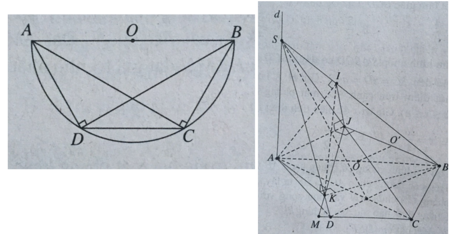
Hình thang ABCD có hai cạnh bên và đáy nhỏ bằng nhau và bằng nửa đáy lớn, nên nó là nửa lục giác đều nội tiếp trong đường tròn đường kính AB, tâm O là trung điểm của AB.
Như vậy: ∠(ACB) = ∠(ADB) = 1v.
a) Theo giả thiết, ta có: SA ⊥ (ABCD) ⇒ SA ⊥ BC
BC ⊥ SA & BC ⊥ AC ⇒ BC ⊥ (SAC) ⇒ BC ⊥ SC. (1)
Mặt khác SB ⊥ (P) nên SB ⊥ IJ (⊂ (P)) (2)
Từ (1) và (2) suy ra BCJI là tứ giác nội tiếp trong đường tròn đường kính BJ.
Ta có BC ⊥ (SAC) ⇒ BC ⊥ AJ (⊂ (SAC))
AJ ⊥ BC & AJ ⊥ SB (do SB ⊥ (P)) ⇒ AJ ⊥ (SBC) ⇒ AJ ⊥ JI (⊂ (SBC)) (3)
Lý luận tương tự, ta có:
BD ⊥ AD & BD ⊥ SA ⇒ BD ⊥ (SAD) ⇒ BD ⊥ AK (⊂ (SAD))
AK ⊥ BD & AK ⊥ SB(⊂ (P)) ⇒ AK ⊥ (SBD) ⇒ AK ⊥ KI. (4)
Từ (3) và (4) suy ra AKJI nội tiếp trong đường tròn đường kính AI nằm trong mặt phẳng (P).
b) Ta có ngay O’ là trung điểm BJ
Vì OO’ là đường trung bình của ΔABJ nên OO’ // AJ
Mà AJ ⊥ (SBC) nên OO’ ⊥ (SBC)
c) Ta có (SCD) ∩ (ABCD) = CD.
Gọi M = JK ∩ CD
SA ⊥ (ABCD) ⇒ SA ⊥ AM(⊂ (ABCD)) (5)
SB ⊥ (P) ⇒ SB ⊥ AM (⊂ (P)) (6)
Từ (5) và (6), ta có: AM ⊥ (SAB) ⇒ AM ⊥ AB.
Suy ra AM là tiếp tuyến của đường tròn ngoại tiếp ΔABC tại A. Như vậy AM cố định. Vì M = AM ∩ CD nên M cố định.
d) ΔAIB vuông tại I nên OA = OB = OI
ΔAJB vuông tại J (do AJ ⊥ (SBC)) nên OA = OB = OJ).
ΔAKB vuông tại K (do AK ⊥ (SBD)) nên OA = OB = OK).
Ta có OA = OB = OC = OD = OI = OJ = OK nên O là điểm cách đều các điểm đã cho và OA = AB/2 = a.
e) Theo chứng minh câu c.
f) Khi S thay đổi trên d, ta có I luôn nằm trong mặt phẳng (B, d).
Trong mặt phẳng này I luôn nhìn đoạn AB cố định dưới góc vuông nên tập hợp I là đường tròn ( C 1 ) đường kính AB nằm trong mặt phẳng (B, d).
Tương tự, tập hợp J là đường tròn ( C 2 ) đường kính AC nằm trong mặt phẳng (C, d) và tập hợp K là đường tròn đường kính AD nằm trong mặt phẳng (D, d).

a) góc MAN nội tiếp chắn nửa (O) => góc MAN = 900 hay góc CAD = 900
tam giác CAD vuông tại A có đường cao AB => AM.AC = AB2 = 4R2 không đổi
b) Tam giác OAN có OA = ON = R nên cân tại O => góc OAN = góc ONA hay góc BAD = góc MNA
mà góc BAD = góc ACD (cùng phụ góc BAC) => góc MNA = góc ACD => tứ giác CMND nội tiếp
c) tam giác ACD vuông tại A có AI là trung tuyến => IA = ID = 1/2 CD => tam giác IAD cân tại I => góc IAD = góc IDA
mà góc IDA = góc AMN( tứ giác CMND nội tiếp) => góc IAD = góc AMN mà góc AMD phụ góc MNA => góc IAD phụ góc MNA
=> góc AHN = 900 hay góc AHO = 900 , mà OA = R không đổi => H nằm trên đường tròn đường kính AO
a﴿ góc MAN nội tiếp chắn nửa ﴾O﴿ => góc MAN = 90o hay góc CAD = 90o
tam giác CAD vuông tại A có đường cao AB => AM.AC = AB 2 = 4R 2 không đổi
b﴿ Tam giác OAN có OA = ON = R nên cân tại O => góc OAN = góc ONA hay góc BAD = góc MNA
mà góc BAD = góc ACD ﴾cùng phụ góc BAC﴿ => góc MNA = góc ACD => tứ giác CMND nội tiếp
c﴿ tam giác ACD vuông tại A có AI là trung tuyến => IA = ID = 1/2 CD => tam giác IAD cân tại I => góc IAD = góc IDA
mà góc IDA = góc AMN﴾ tứ giác CMND nội tiếp﴿
=> góc IAD = góc AMN mà góc AMD phụ góc MNA => góc IAD phụ góc MNA
=> góc AHN = 90 0 hay góc AHO = 90 0 , mà OA = R không đổi => H nằm trên đường tròn đường kính AO
Gọi I là giao điểm của hai đường chéo của hình thoi. Chứng minh P là trọng tâm của ∆ABC
Kẻ PQ//AI => BQ = 2 3 AB => Q Cố định => P thuộc đường tròn đường kính QB